目次ページ 前ページ 次ページ
14. 立体図形の射影変換
14.3 透視図に使う三次元射影変換
14.3.4 面方程式の射影変換を考える
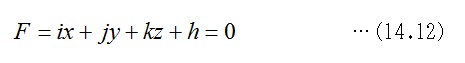
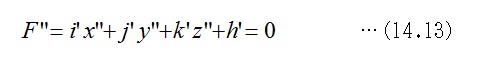
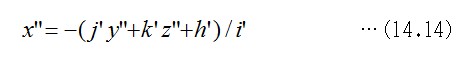
目次ページ 前ページ 次ページ |
14. 立体図形の射影変換 |
14.3 透視図に使う三次元射影変換 |
14.3.4 面方程式の射影変換を考える |
多面体を構成する一つの多角形面に注目すると、それを構成する頂点座標は、幾何学的な一平面に載っています。その面方程式の一般形は、第11章の式11.4で解説しました。変換前の面を表す定数パラメータの記号に、上で使った英字記号との重複を避けて、下のように書くことにします。
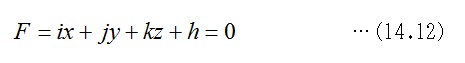 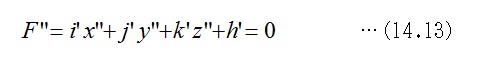 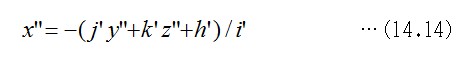 2009.2 橋梁&都市PROJECT |
前ページ 次ページ |