目次ページ 前ページ 次ページ
14. 立体図形の射影変換
14.3 透視図に使う三次元射影変換
14.3.5 逆変換の関係式が必要になること
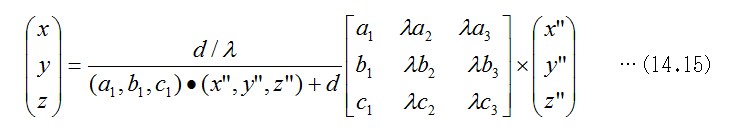
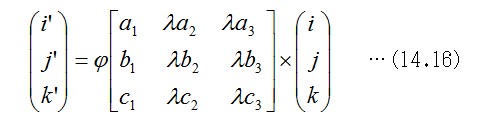
目次ページ 前ページ 次ページ |
14. 立体図形の射影変換 |
14.3 透視図に使う三次元射影変換 |
14.3.5 逆変換の関係式が必要になること |
三次元の射影変換をすると、座標軸の向きは直交性が満たされない変換を受けます。したがって、元の座標(x,y,z)を変換後の座標(x",y",z")で表す逆変換を求めておいて、それを式14.12に代入して射影変換後の面方程式14.14を求めます。射影変換の変換と逆変換とは相対的ですので、式14.11の逆変換の一般的な式は、下のような形で提案することができます。
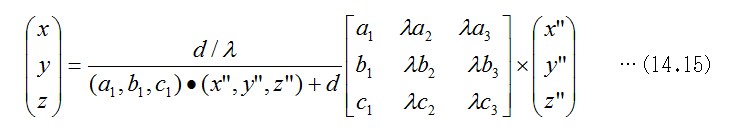 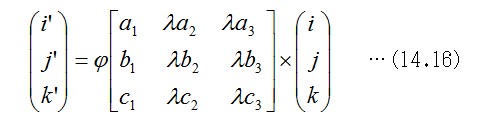 2009.2 橋梁&都市PROJECT |
前ページ 次ページ |