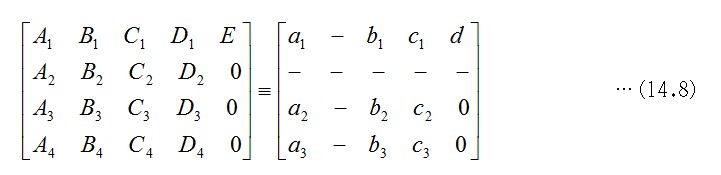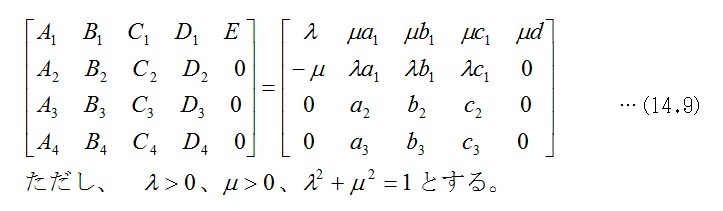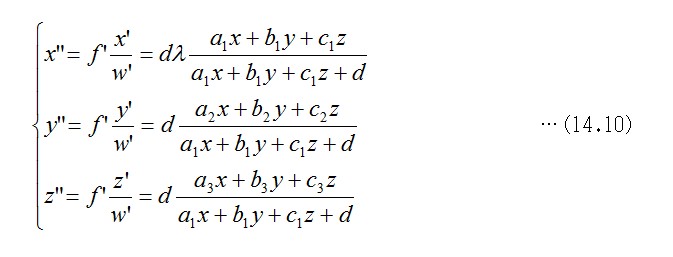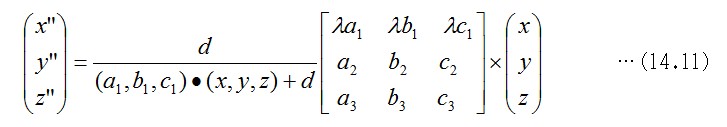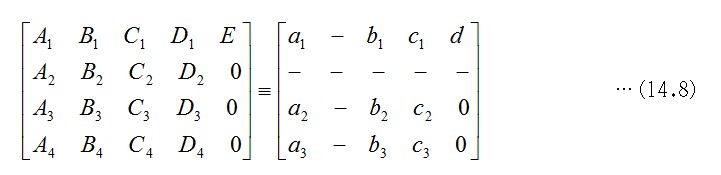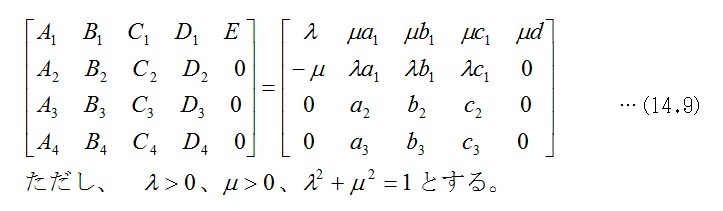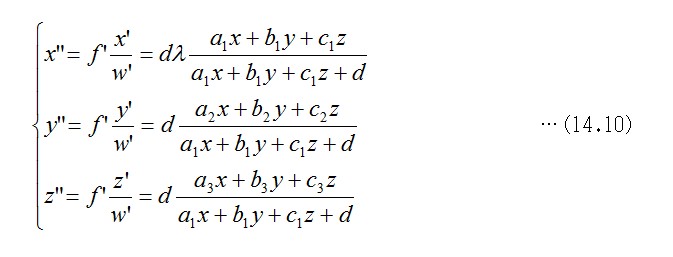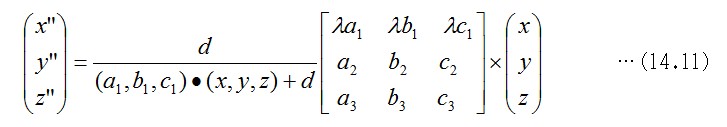一般的に線形代数の問題を扱うとき、或る座標軸成分を考えないか、0または定数と置くと、次元数が一つ下がります。三次元の射影変換の対象に切り紙を考えると、変換の結果を二次元の射影変換と同じ式にすることができます。擬似的な四次元平面の中には、現実的な三次元座標(x,y,z)があります。ここに在る切り紙は、任意の向きを考えることができますが、平面図形の射影変換を考えるときの切り紙は、x座標を定数とします。切り紙を斜めからカメラが見るように回転させて変換するのは、切り紙を擬似的な四次元平面に載せた全体で回転させます。三次元の射影変換は、式14.4ですが、x"を無視して(y",z")だけに注目すれば、前章の二次元図形の射影変換式式13.4で示した(y",z")を表す式と同形にすることができます。平面図形の場合は、便宜的にｘ軸を奥行き方向を表す座標軸としましたが、ｘの文字記号をｗに置き換えて式の整合を取ります。この整合は、変換式のパラメータ間の対応関係をまとめて理解するために、４×５のマトリックスで表します。
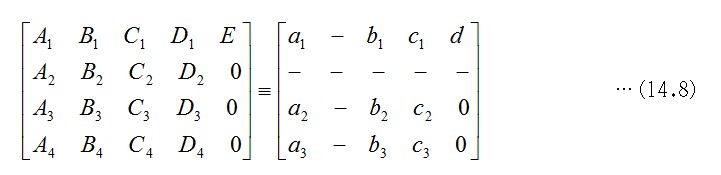左辺のマトリックス成分の中、ｘ軸の座標を求める第２行と第２列に対応する右辺のマトリックス成分がありません。そこで、この成分を補うことを考えます。座標軸の向きを示すベクトルが単位ベクトルであることと、直交性を満たすように、左辺のマトリックス成分を下のように提案します。
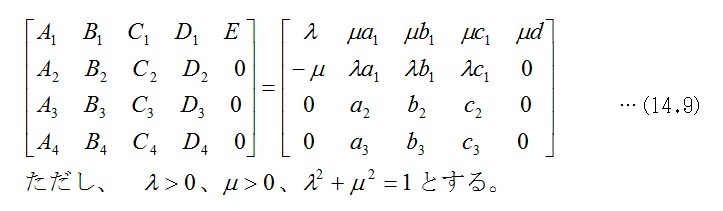式14.9の左辺４×４のマトリックス部分は、行・列ともに単位行列で直交性を満たします。式14.4と式13.4とを一致させるには、x=0, f'=μf とすればよいことが分かります。λの値は、前の14.2.4節で紹介したように、レンズの視角と関連を持ちますので、λ＝Ａ1=0.7を一つの参考値とします。式14.9の右辺のパラメータを代入して式14.4を書き直した式を示します。
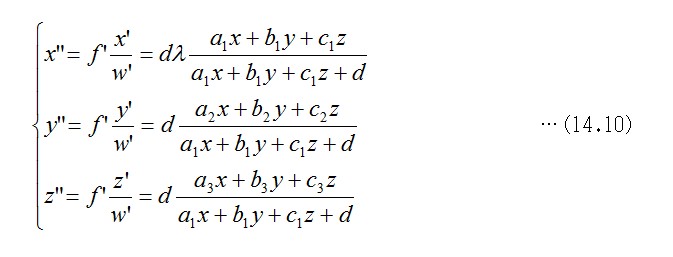式14.5と同じようにベクトルとマトリックスを使う表し方で書き直します。
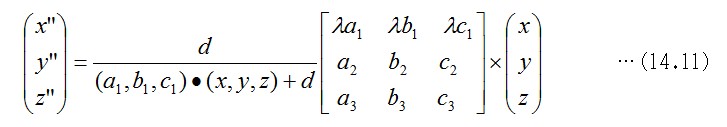
2009.2 橋梁＆都市PROJECT |