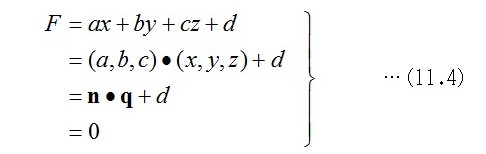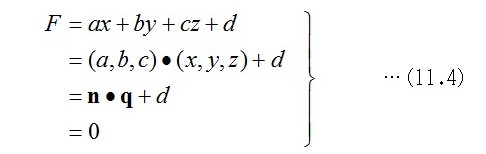代数幾何学的に平面を表す一つの方法は、式(11.1)の行単位で示した同次式です。この式は、全体を一定倍しても同じ意義を持ちます。そこで、４つの定数a,b,c,dに幾何学的、かつトポロジー的な性質を持たせるような約束を決めます。平面を表す式を、下のように、ベクトルを使った式に書き直します。
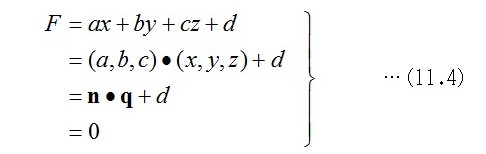上の三行の式は、すべて同じ意味ですが、表現方法を変えた順に書いたものです。二行目は、(a,b,c)と(x,y,z)をベクトルの約束で使います。これらを三行目ではベクトル記号n, qに代えたものです。記号の点（・）は二つのベクトル間の内積（スカラー積）の記号と約束します。すぐ後の項で出てきますが、記号（×）を使うときは外積（ベクトル積）の約束にします。何も記号を挟まないときはベクトルの二項積（diad: 第9.4節参照）を表す量とします。Ｆの幾何学的な意味は、与えられた点の座標(x,y,z)と、この面との符号付き距離を与える式です。単純に距離と言うときは正の値で言うのですが、座標幾何学的に扱うときは、向きを考えて、負の距離と言う概念が必要になります。四行目Ｆ=0は、その点が面上にある条件です。単位ベクトルnを、この面の法線ベクトルとします。ベクトルは向きを持ちますので、法線ベクトルは面の裏から表に向かうと約束することで、面の裏表の区別を決めます。そうすると、dは、世界座標の原点(x=y=z=0)が、面からdの距離に在ることになります。そうすると、原点から面に垂線を降ろした交点の座標が -dｎとなりますので、これをこの面の基点（または代表点）と約束することにします。
2008.11 橋梁＆都市PROJECT |