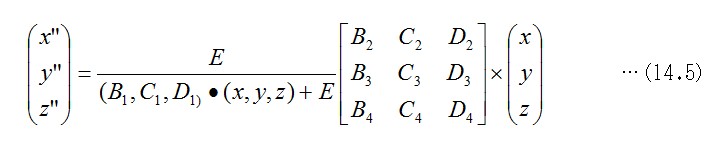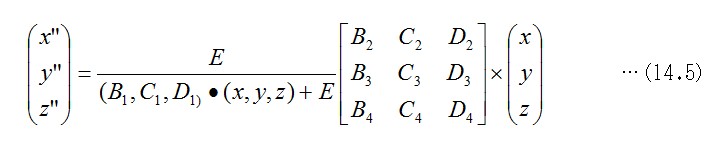式14.4は、パラメータが込み入っていますので、同じ意味ですが、マトリックスとベクトルを使った表し方を下に示します。寸法変化がほぼ１：１になるように標準化しました。
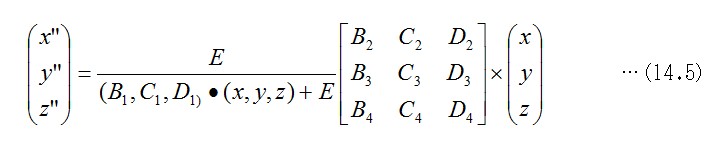この式の幾何学的な意味を説明します。右辺の３×３のマトリックスは、座標変換を行わせる意義を持ちますが、アフィン変換を表していて、回転と、拡大または縮小変形を行わせます。ただし、この行ベクトルの寸法は、単位長さよりも小さな値です。これは、元になった式14.1の４×４マトリックスが、その行ベクトルのノルムを１に標準化してあるからです。また、この変換は、必ずしも直交座標変換ではありません。マトリックスのスカラー倍を与える分数式の分母には、位置ベクトル(x,y,z)と、カメラの向きから決まる方向ベクトル(B1,C1,D1)との内積があります。方向ベクトルも単位長さではありません。このベクトル方向は、図形がすぼむ方向を与えます。この分母の式全体は、(B1,C1,D1)を座標軸と考えて、図形の座標位置(x,y,z)と視点との余弦距離の意義を持ちます。この距離に反比例して、変換された座標全体の寸法がすぼみます。Eの絶対値を十分に大きくするのは擬似的な望遠レンズを使うことです。射影変換の特徴が小さくなり、アフィン変換に近づきます。分母の一次式を最初から定数にする条件は、単純な回転を与えます。
2009.2 橋梁＆都市PROJECT |