目次ページ 　 前ページ 　次ページ

2.　数学と算術との対立

2.3　数の丸めを理解する

2.3.3　閾値を理解する

　難しい漢字を使いますが、しきいち（敷居値）と読みます。英語はthresholdです。日本住宅では部屋の境に普通に見かける構造ですが、英語では鴨居の意義もあります。敷居は、幅の無い境界線ではなく、ある寸法幅を持つことに注意します。この用語は、代数的な方法を応用する座標幾何学で見られるようになりました。原理を言えば、幾何学的な２点間の距離が、閾値よりも小さければ、実質的に同じ点と見なす実用的な判断に使います。数値計算では、丸めの処理に現れます。丸められた数値は、最後の桁に±0.5の誤差を含みます。これは、最後の桁位置で、幅１の閾値を考えることです。実用的に最も良く使われる丸めは、小数を含む実数を整数に丸めるときです。これを図2.1で説明します。

図2.1　実数を整数化するときの敷居値の位置


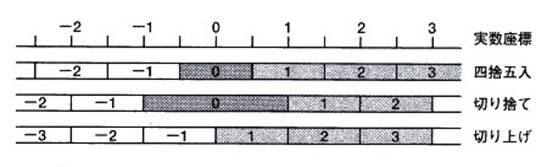
　この図の最上段は、実数の大小を表す一次元の直線座標を表しています。整数位置に目盛を付けてありますが、中間の0.5にも補助目盛を付けてあります。整数に丸めると、同じ整数になる実数座標の範囲が、丸めの約束によって異なります。例えば整数の１を表す実数の座標範囲が異なることを見て下さい。一見して分かるように、四捨五入では、閾値の幅がすべて同じであるのに対して、切り捨ては０の幅が２倍に、切り上げは０の区間がありません。
前ページ 　次ページ