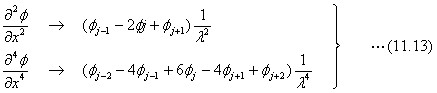目次ページ 前ページ 次ページ |
11. 数理弾性学 |
11.3 二次元弾性体の解析 |
11.3.6 微分式に代えて差分式も研究される |
微分方程式 (differential equation)に出発して、解析的に解が得られるのは、実は非常に条件に恵まれた場合です。そうであっても、具体的に数値として計算する段階で、計算技術でも多くの課題があります。応力を計算したい座標は、実際には或る飛び飛び(離散的：discrete)の位置です。そこで最初から離散的な位置で理論式を構成することも研究されてきました。その一つが差分方程式（階差式：difference equation）での表現です。梁の解析の場合には、微分方程式の解と正確に一致する結果が得られるような差分式の表現法があります。クラペーロン(B.P.E.Clapeyron, 1799-1864)の論文が基礎になった三連モーメント式(three moments theorem)がその例です。差分方程式を二次元弾性体の解析に応用するときは、梁の場合のような厳密解を提案することができませんので、近似計算法として実用されます。微分方程式を階差式で近似するときは、偶数階の微分方程式を扱うときに扱い易い形になります。一定間隔λの注目点では、微分方程式と差分方程式とを次の形で対応させます。注目点の座標位置は整数座標ｊです。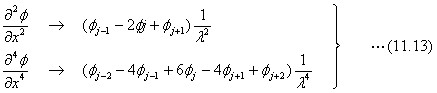 ここまでの解析研究は、コンピュータが利用できるようになって大きな変化が起こりました。その代表が有限要素法（ＦＥＭ）の利用です。ＦＥＭは、差分方程式の考え方の延長に位置づけることができます。しかし、注目点を選ぶとき、任意図形の境界条件に合わせるように注目点を選ぶ自由度があるのが便利です。ただし、ＦＥＭも近似計算法の性格がありますので、計算結果の評価について、正確な解析法との誤差が論議の種になります。 科学書刊株式会社:電子版 「橋梁＆都市 PROJECT: 2011」 |
前ページ 次ページ |