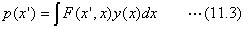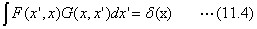目次ページ 前ページ 次ページ |
11. 数理弾性学 |
11.2 均質な弾性体の解析モデル |
11.2.6 数値計算にはマトリックスが使われる |
具体的に梁の変形を数値として計算したいときは、注目点を、連続座標ではなく、有限個数の、或る飛び飛び(discrete)の座標位置で考えます。そうすると、実用的にはマトリックスを扱います。式(11.1)は概念式です。数値計算に使うときは、或る個数の有限個の注目点での解を扱いますが、これがマトリックス形での表現になります。式(4.1),(4.2)の表し方を見て下さい。これは、二変数関数Ｇ（ｘ、ｘ’）をマトリックスの形で表した例です。これをＦＥＭでは変位のマトリックス(flexibility matrix)と言います。このマトリックスの逆マトリックスが得られれば、任意の変形が与えられたときの荷重の大きさが一意に決まります。ここで、「逆マトリックスが得られれば」と仮定法で説明したことに注意して下さい。コンピュータを使うとしても、数値計算の場では、注目点の数が非常に多くなると、逆マトリックスの計算結果が実際には誤差が大きくなって使いものにならないことが起こります。元のグリーン関数で逆マトリックスに相当する表現式は、下の形で提案できます。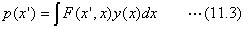 ここでのＦ（ｘ’、ｘ）は逆マトリックスに相当する関数とします。そうであると、元のマトリックスと逆マトリックスとの積が単位行列になることの関係式は、下の式の形になるはずです。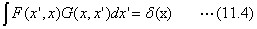  いま、単純梁を例として考えます。Ｇ（ｘ’、ｘ）のフーリエ級数解が得られたとした場合、高次のフーリエ係数の大きさは微小になっていきます。Ｆ（ｘ’、ｘ）のフーリエ級数解の係数は、逆に高次の項が無限に大きくなっていきますので、数値計算に使うことができる意味の有る解は得られません。 科学書刊株式会社:電子版 「橋梁＆都市 PROJECT: 2011」 |
前ページ 次ページ |