目次ページ 前ページ 次ページ
10. 衝撃・振動・疲労
10.5 疲労実験データの整理
10.5.4 応力度振幅の関係を求める
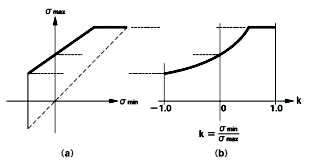疲労を考えて部材の断面設計をするときは、部材に作用する応力の方の振れ幅を予測しておいて、材料の許容応力度を決めます。例えば、トラス橋の設計では、弦材ごとに影響線を求めておいて、最大・最小の軸力（Ｓｍｉｎ，Ｓｍａｘ）を計算します。ここで、（Ｓｍｉｎ／Ｓｍａｘ）を、図10.5の（σｍｉｎ／σｍａｘ）と同じ値になるように許容応力度σｍａｘを決めたいとします。これが第三段階の整理です。図10.6bは、この提案を使い易いグラフにまとめたものです。このグラフを作成するときは、図10.5のグラフを、数式に載せやすいように抽象化した図10.6aに書き直します。応力度の振幅を表すパラメータを、ｋ＝（σｍｉｎ／σｍａｘ）で置き換えます。ｋ＝-1は両振れ、ｋ＝0は片振れ、ｋ＝1は静的強度（降伏点）です。応力度の振幅が小さい範囲は疲労限を降伏点に置くことにして、疲労限σｍａｘをσｍｉｎの一次式で表します。そうすると、疲労限σｍａｘは、下の式で表すことができます。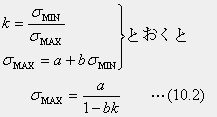
図10.6bのグラフを、ほぼ相似にして、鉄道橋では許容応力度の提案式に使っています。材料の降伏点に対して採用した安全率を、疲労を考える場合の安全率にも準用します。ｋの値は、部材の応力振幅の計算値（Ｓｍｉｎ／Ｓｍａｘ）を代入します。