目次ページ 前ページ 次ページ
10. 衝撃・振動・疲労
10.3 疲労破壊の全体概念
演習例題 10.1
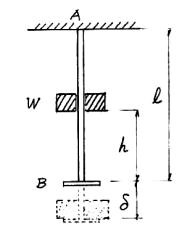(1) 図10.3において、ＡＢは、長さＬの弾性的な鋼棒である。Ａ点で固定され、Ｂにフランジがついている。錘Ｗは、棒をガイドとして、高さｈから落下させる。錘は、衝撃的にＢを介して棒に力が作用し、或る最大撓みδを生じる。この撓みを求めよ。ここに、鋼棒の断面積Ａ＝20cm2、ヤング率Ｅ＝2.1×106 kgf/cm2、Ｗ＝2t、Ｌ＝5m、ｈ＝5cm、とする。(2) 錘の衝突後はリバウンドで錘は跳ね上がり、或る高さｈ’に戻るとする。現象としては、この高さからの落下が起きて、何度かの衝突が繰り返される。リバウンドによる位置エネルギーが消費される分は、鋼棒の運動エネルギーになり、これは鋼棒の縦振動になる。この振動数と加速度（応力波）を求めよ。
解説：
この問題は、段階的な思考実験に適しています。まず、第一段階として、静的に錘Ｗを吊り下げたときの鋼棒の解から始めます。断面の応力度をσ、そのときの撓みをｙとします。
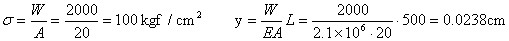
錘Ｗが最初の衝突で静止したとき、「錘の位置エネルギー分Ｗ（ｈ＋δ）が棒の弾性エネルギーＵと等しい」とする条件を考えると、下の式が得られます。
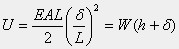
この式は、δの二次式です。解は下の式です。ここにｙは、上の静的な撓みです。
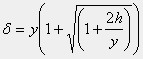
上の式は、次のように解釈します。ｈ＝0であるときは、錘をフランジに接した状態で離すことですので、δは、静的撓みの２倍です。静的に荷重を作用させた状態で、付加的な変位を与えるときは、ｈを負の数とします。ｈ＝5cmであると、静的な撓みの21.52倍の撓みですので、σ＝2152kgf/cm2です。この問題を、錘Ｗの衝突とすると、フランジに接触するときの速度は、ｈ＝5cmを落下するとして
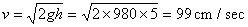
錘の落下衝突によって、錘はリバウンドでｈ’に撥ね上がるとします。ポテンシャルエネルギーの差、ΔＵ＝Ｗ（ｈ−ｈ’）が鋼棒システムに伝わります。このシステム全体が完全な弾性体であるとして、このエネルギーが鋼棒の弾性エネルギーに使われたとします。鋼棒は、静力学的には応力度がありませんが、縦振動で伸縮すれば応力度が発生しますので、その弾性エネルギーを求めることができます。そのときの最大応力度をσ’と置くと、
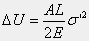
リバウンド量をｈ’＝0.5ｈと仮定すると、応力度は次式で得られます。
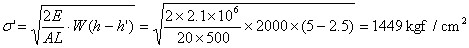
鋼棒は、その長さを伝わる縦波（音としての振動）があります（10.2.3節参照）。その速度は5120m/secです。この速度で弾性波が鋼棒を１往復する周期で鋼棒が振動すると、周波数は512Hzです。この動的な応力度σ’は、鋼棒の上端Ａで逃げてしまいますので、振動が減衰します。