目次ページ 前ページ 次ページ
9. 材料の破壊と部材の破壊
9.2 破壊の力学モデル
9.2.4 鋼材の破壊モデル
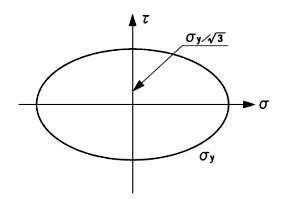鋼材料、一般的には金属材料、の強度は、引張と圧縮とを応力度の正負で考えるだけで同じ性質があると仮定します。鋼材は、降服点を超えると塑性的な変形が続きます。これは、部分的に応力度が大きくなる個所を平均化して行きます。引張試験をすると、断面の応力度分布の変化が最も小さくなる、試験片のほぼ中央部で破断します。この事象の説明が、ミーゼズ(R. von Mises)の歪みエネルギー一定説です。応力度分布が一様である個所は、全体の歪みエネルギーが最小になる個所であって、そこで全体破壊が生じると考えれば、引張試験片の破断がほぼ中央で起こることが説明できます。材料が降服点に達すると、体積変化のない変形が始まります。これはポアソン係数νが0.5になった状態です。鋼構造物では薄板を二次元応力状態で使うことが多いことを考えて、二方向の主応力度と剪断応力度で表せる下の式が、材料の引張試験で得られる降伏点σyに達したときを、破壊が始まる条件とします。
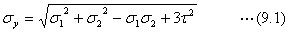
主応力度一つと剪断応力度の組み合わせを考えるとき、例えば、プレートガーダーのウエブ上端は、破壊条件が下の式 (9.2)のような楕円式になり、グラフに描くと図9.4のような楕円が破壊条件を表します。
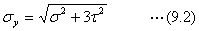
純粋な剪断応力の場では剪断応力度が降伏点の0.58倍で生じる計算になります。鋼材の剪断許容応力度は、これを根拠として、引張許容応力度の約58％を提案しています。