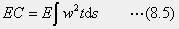目次ページ 前ページ 次ページ
8. 剪断応力度に関する特殊な問題
8.3 棒の捩じれ
8.3.5 薄肉断面の反りは二種類ある
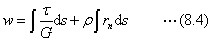
ここにrn×ds、板幅方向の微小長さの部分の、回転中心に関する能率(モーメント)です。図8.11のパイプ断面(閉じた断面と言います)でも、幾何学的な反りがあります。これは、図8.11の右の図で破線で示した線です。この反りは、断面を一周すると、反りが元に戻りますので、幾何学的な原因によって生じる反りの大部分が打ち消され、剪断応力度による歪みが反りの主な要因です。一方、図8.12のH断面は、開いた断面ですので、板幅方向の剪断歪みによる反りは小さく、幾何学的な要因による反りが主役になることが理解できると思います。捩じれを受けるこの部材端を別の部材と繋ぎたいとき、この反りを拘束し、断面図形が平面を保つように接続すると、接続箇所に大きな局部応力度が発生することが予想できます。H形部材のフランジ部分は、捩じれは板面内の曲げを受けることが理解できると思います。実際の構造物の詳細設計では、意図的に剛な接続を避ける構造も見られます。このような幾何学的な反りを考えて解析することは、航空機のような薄肉部材の座屈を考えるときに必要になりました。この先駆的な研究はワグナー(H. Wagner)でしたので、サンブナンの捩じりと対応させる意味で、この捩じれをワグナーの曲げ捩じれと言うことがあります。曲げ捩じれを考えるとき、曲げ剛性をEJと表すことに似て、曲げ捩じれ剛性ECを計算します。この計算式も概念式の紹介に止めますが、ρ=1の場合の反りからの弾性エネルギー式の形になります(後の第8.4.3項も参照して下さい)。