目次ページ 前ページ 次ページ
8. 剪断応力度に関する特殊な問題
8.4 剪断流の不静定問題
8.4.1 非対称の箱桁断面の剪断中心
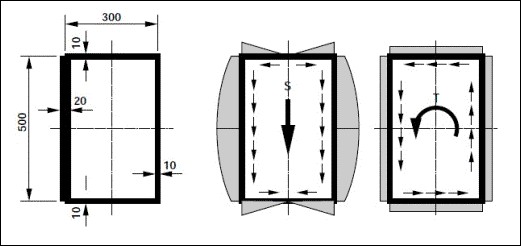
図8.13 空間直線の定義を示す見取り図
目次ページ 前ページ 次ページ |
8. 剪断応力度に関する特殊な問題 |
8.4 剪断流の不静定問題 |
8.4.1 非対称の箱桁断面の剪断中心 |
図8.13に、具体的な寸法を持った箱桁断面を計算例題として使って、ここでの問題を説明します。この断面の、図形としての重心位置、断面二次モーメントは、第4章で紹介した方法で計算することができます。曲げモーメントによる各部の応力度の計算も、問題がありません。しかし、両側のウエブは、二つの桁を繋いだと見ることができますが、箱桁全体に掛かる剪断力を、左右のウエブで分担する割合が不静定です。つまり、第7.3節で解説した剪断中心の位置と、重心の位置とは同じになりません。これを解く条件は、箱断面の剪断応力度から、箱断面を一周して反りが元に戻ることです。最初、仮に断面の中心を剪断力の作用線が通るとして、左右のウエブには等しい剪断力を割り振ります。この状態で、箱断面を一周する反りを計算します。この反りが0でなければ、単純捻じれ相当の一定剪断流によ反りで打ち消すようにトルクを加えます。理屈はそうですが、これも具体的な数値計算に使う代数式を提案するよりも、手計算の感覚を生かして計算手順を組み立てるのが実践的な解決です。この章の始めに紹介したように、以下に例題の数値計算をまとめました。 図8.13 空間直線の定義を示す見取り図 科学書刊株式会社:電子版 「橋梁&都市 PROJECT: 2011」 |
前ページ 次ページ |