目次ページ 前ページ 次ページ
8. 剪断応力度に関する特殊な問題
8.1 曲げを受ける梁の剪断応力度によるソリ
8.1.2 剪断を受ける矩形断面の梁
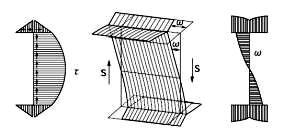
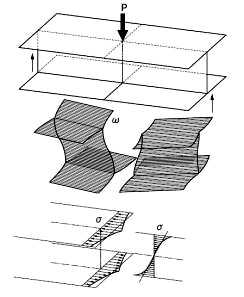
図8.1 反りによる軸方向の変形 図8.2 左右の反りが食い違う場合
図8.1に示すような、薄肉のI形の梁を考え、断面の剪断応力度の分布をまず描きます(図8.1a)。剪断応力度を受ける二次元の応力状態の板は、第3.2節で説明したように、矩形が平行四辺形に変形します。それがどのように桁断面に現れるかを、やや強調して見取り図に描いたものが図8.1bです。この図では、梁の長手方向を水平にしましたので、断面各部は垂直な断面から長手方向に移動し、断面全体は平均して或る微小角度だけ傾きます。これが梁としての剪断変形です。図8.1cは、断面各部の移動の状態を、薄板を座標軸にして関数図形のように作図したものです。ウエブの剪断応力度分布は放物線ですので、移動量を示すグラフは三次曲線です。フランジでは剪断応力度分布が直線ですので、移動量を示すグラフは二次曲線です。長手方向の移動量全体は、平行移動分と回転分と持ちます。これを引いた変形分が断面の反りです。今、図8.2のような薄肉断面部材を考えて、中央に集中荷重を作用させます。中央に対して左右の梁の剪断力は、向きが反対です。この桁は集中荷重の作用位置で折れ曲がるように接続します。しかし、反り分は、このままでは繋がりません。実構造では、断面変形を抑える剛な隔壁などを介します。したがって、この反りを打ち消すように、軸方向に二次的に垂直応力度が発生します。これが剪断遅れです。これは、サンブナンの原理が適用できる局部的な応力度です。