目次ページ 前ページ 次ページ
5. 弾性的性質の数学モデル
5.2 線形弾性として扱う便宜的な方法
演習例題 5.1
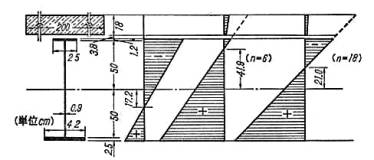
図5.2は、死活荷重合成桁とした断面計算の一例です。コンクリートのヤング率を変えた二種類の断面定数の計算法を示します。応力度の計算は、全死荷重モーメント63tf-mを受けるとき、鋼桁だけで受けるとしたとき、完成直後(n=6)、クリープ発現後(n=18)の各場合を比較したものです。
種 類 |
A (cm2) |
y(cm) |
Ay(cm3) |
Ay2(cm4) |
J0 (cm4) |
(kgf/cm2) |
コンクリート(200×18) |
3600 |
64 |
230400 |
14745600 |
97200 |
|
コンクリート(n=6) |
600 |
64 |
38400 |
2457600 |
16200 |
|
コンクリート(n=18) |
200 |
64 |
12800 |
819200 |
5400 |
|
(25×1.2) |
30 |
50.6 |
1518 |
76810 |
-- |
|
鋼(1000×0.9) |
90 |
0 |
0 |
0 |
75000 |
|
鋼(42×2.5) |
106 |
-51.25 |
-5381 |
275790 |
55 |
|
鋼桁 |
225 |
-3863 |
427655 |
|||
|
e=-3863/225=-17.2 cm IS=427655-17.2×3863=361000 cm4 WSU=-361000/68.4=-5280 cm3 WSL=361000/35.3=10230 cm3 |
σSU=-1193 σSL=616 | |||||
合成桁(n=6) |
825 |
34537 |
2900455 |
|||
|
e=34537/825=41.9 cm Iv=2900455-41.9×34537=1453000 cm4 WCU=(-1453000/31.1) ×6=-280000cm3 WCL=(-1453000/13.1) ×6=-665000cm3 WSU=-1453000/9.3)=-156000 cm3 WSL=1453000/94.4)=15390 cm3 |
σCU=-23 σCL=-9 σSU=-40 σSL=409 | |||||
合成桁(n=18) |
425 |
8937 |
1251255 |
|||
|
e=8937/425=21.0 cm Iv=1251255-21.0×8937=1064000cm4 WCU=(-1064000/52.0) ×18=-368000cm3 WCL=(-1064000/34.0) ×18=-563000cm3 WSU=-1064000/30.2)=-35230 cm3 WSL=1064000/73.5)=14480 cm3 |
σCU=-17 σCL=-11 σSU=-179 σSL=434 | |||||