目次ページ 前ページ 次ページ
3. 二次元弾性体の応力と変形
3.2 主応力と主ひずみ
演習例題 3.2
図3.13 鋼材の引張り試験片
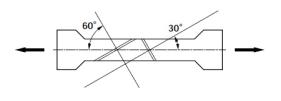（解：30°の場合σｎ＝1350、τ＝779。60°の場合、σｎ＝450、τ＝779。単位はkgf/cm2である。）解説：この問題は、式(3.1)を利用して計算できますが、同時に、モール円（図3.6）を描いて、図式で数値の確認をすることを奨めます。材料試験機の秤量表示は、重量トン表示からキロニュートン表示に変っていますので、重力加速度9.8で除した値を使うようになりました。したがって、1800kgf/cm2は、約180kNです。材料試験を観察していると、材料が降伏点を超えると、長さ方向に塑性歪みが起きます。引張強度よりも剪断強度が小さいので、直ぐには破断しないで、ミクロのレベルでは約45°方向の剪断滑りが何重にも重なって全体断面が減少していきますが、直ぐには破断しません。これは、材料の結晶レベルで転位(dislocation)が起きているためです。引張り強度に持たなくなる荷重になると、長手方向に直角の断面で破断します。破断するときの断面積は、元の断面積よりも小さくなっていますが、実用的な引張強度相当の応力度は、元の断面積当たりで表します。鋼材に塑性加工を加えて圧延すると、相対的に断面が減少した材料になり、結果的にこの材料の引張強度が上がります。なお、コンクリートの圧縮試験は、力の符号が逆になります。この材料は、剪断強度が圧縮強度よりも小さいので、45°方向の面で滑り破壊が起きます。
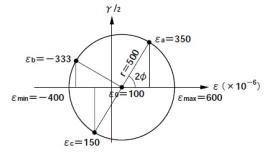
BR> (2)図3.11に示したような配置のロゼットゲージを使って応力測定をして、三方向の歪みが左回りに45°の順で、εａ＝350×10-6、εｂ＝−333×10-6、εｃ＝−150×10-6、と得られた。主歪みの大きさ、向き、を求めよ。これから、主応力の大きさを求めよ。ただしヤング率Ｅ＝2.1×106kg/cm2、ポアソン比ν＝0.3とする。
例解：第3.2.7項で解説した手順で計算します。歪みのモール円は図3.14に示します。
歪みのモール円の中心座標： ε０＝(350×10-6−150×10-6)/2＝100×10-6
εａ−ε０＝350×10-6−100×10-6＝250×10-6
ε０−εｂ＝100×10-6−(-333×10-6)＝433×10-6
歪みのモール円の半径（式3.7）：ｒ＝sqrt(2502＋4332)×10-6＝500×10-6
主歪みの偏角（式3.8） φ＝0.5×tan−１（433/250）＝30°
主歪みの大きさとと向き εＭＡＸ＝100×10-6＋500×10-6＝600×10-6（x軸）
εＭＩＮ＝100×10-6−500×10-6＝−400×10-6（ｙ軸）
全体を右回りに15°回転した向
主応力の大きさ（式3.3b） 2.1/(1−0.32)＝2.3
σＭＡＸ＝2.3×(600−0.3×400)＝480kg/cm2（x軸）
σＭＩＮ＝2.3×(−400＋0.3×600)＝−220 kg/cm2（ｙ軸）
図3.14 3.14 三方向歪みのモール円の解、 図3.15 ロゼットゲージの歪みと主軸方向
