目次ページ 前ページ 次ページ
3. 二次元弾性体の応力と変形
3.2 主応力と主ひずみ
3.2.7 モール円を応用して主歪みの向きと大きさを求める
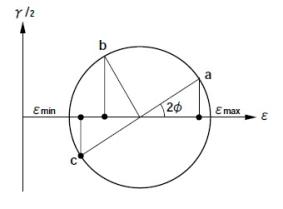ロゼットゲージを使って３方向の歪みを測定したとして、測定個所の主歪みの大きさと向きを求めるときは、測定個所の座標系の約束、ロゼットゲージの向きの約束、などの幾何学的な条件を決めておかないと、結果を間違って判断することがあります。したがって、後で説明する代数式を使う場合でも、あらかじめ、歪みの性質をモール円で表した場合の対応を理解しておく必要があります。まず、ロゼットゲージの番号、図3.11ではa,b,cの順番を、aを起点として45°ずつ左周りとします。ゲージaの向きを、測定個所のx軸に合わせ、ゲージcをｙ軸に合わせるとします。この状態で歪みを測定し、歪みがεａ、εｂ、εｃと得られたとします。ここで、この歪みの、モール円の円周上の位置が、図3.12のようになっていたとして、主歪みの大きさと角度φとの関係を吟味しましょう。・モール円の直径2rは、図3.9に示す最大最小の主歪みの差 (εＭＡＸ−εＭＩＮ)/2です。
・モール円の中心は、ε軸上にあり、その位置はε０＝(εＭＡＸ＋εＭＩＮ)/2です。
・モール円の円周上に、90°ずつ左周りに三点があり、そのε座標値がεａ、εｂ、εｃです。
・モール円の中心位置はε０＝(εａ＋εｃ)/2です。
・主歪みの向きは、測定対象の(x,y)座標系から、±45°以内に角度φで振れるとします。
・φの正負の符号は、歪みの大小関係から下の表のように決めます。
| 条件１ | εａ＞εｃ | εａ＞εｃ | εａ＜εｃ | εａ＜εｃ |
| 条件２ | ε０＞εｂ | ε０＜εｂ | ε０＞εｂ | ε０＜εｂ |
| φの符号 | ＋ | − | − | ＋ |
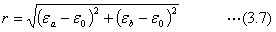
・角度φは
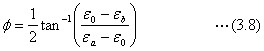
・式(3.8)は、このままで、上で解説したφの符号の約束を満たします。なお、逆正接の数値計算では分母が0に近いときに処理に困ることがあります。EXCELなど、コンピュータの組み込み関数には、ATAN(Y/X)と引数を一つ使う関数と、引数を二つ使うATAN2(X,Y)も使えることを覚えておくとよいでしょう。
・主歪みの向きは、ゲージaの向き（ここではｘ軸）から、角度(−φ)で回転させた方向です。
・主歪みの大きさを、数学的にεＭＡＸ＞εＭＩＮと約束すると、圧縮応力度を主に扱う場合に混乱することがあります。主歪みは、大小順ではなく、歪みの測定値εａとεｃの大小順で判断します。
・主歪みが求まれば、式(3.3b)を使って、主応力の大きさが計算できます。最大剪断応力度は、式(3.2)から分かるように、二つの主応力度差の1/2です。
・モール円の解析は、応力測定の際に扱うことが多いのですが、この目的は局部的な応力の大きさと向きとを知って、部分的な材料の補強方法の提案などに応用します。例えば、コンクリートの場合には、引張り応力に抵抗する向きに鉄筋を入れる；鋼板の補強では圧縮方向の座屈防止に補強する、などが考えられています。