目次ページ 前ページ 次ページ
3. 二次元弾性体の応力と変形
3.2 主応力と主ひずみ
3.2.3 最初に垂直応力度だけによる変形を理解する
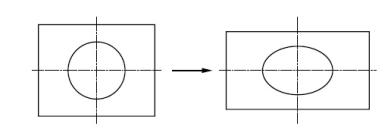二次元弾性体の歪みは、便宜的に垂直応力度による変形と剪断変形とに分けて扱います。剪断変形は、図3.5右に示したように、平行四辺形に変形することです。直交していた四辺形の角度がγだけ変わるとします。この変形を幾何学的に表すためのモデルとして、最初の正方形平面に円を描いておいて、その円が楕円に変形することを想定し、これを数学的に表す方法を求めます。幾何学的に見るとき、円は、長径と短径持つ楕円に変形し、楕円の対称軸は、或る傾斜を持つように変形します。この対称軸方向が主歪みの向きです。剪断応力度が作用しない場合、垂直応力度だけが作用する状態です。これを主応力と言います。円は楕円に変形するのですが、この場合、楕円の対称軸は回転しません（図3.7）。全体が円のまま拡大・縮小するときは、主歪みの向きの傾きを考えるまでもないので、便宜的に元の座標軸方向のままで済ませます。剪断応力が作用しない状態の主応力と歪みの関係は、Ｅをヤング率、νをポアソン比として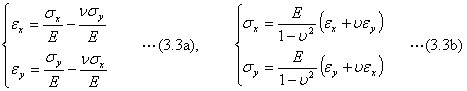
上の式(3.3)は平面弾性体の力学を扱う場合ですので、板の厚み方向の応力σＺを考えません。しかしこの方向にも実はポアソン比分の歪みが出ます。弾性体は、圧縮すれば体積が減ります。側面の応力度が0の状態で柱を圧縮すれば、体積の変化率は（１−2ν）倍に比例します。したがって、物理的に考えて、圧縮して膨張することはありませんので、νの値が0.5よりも大きくはなりません。ゴムは0.5に近い性質を示します。鋼材では約0.3、コンクリートは約0.2、堅い岩石では約0.1です。