目次ページ 前ページ 次ページ
3. 二次元弾性体の応力と変形
3.2 主応力と主ひずみ
3.2.2 座標軸を回転させたときの応力度の表し方
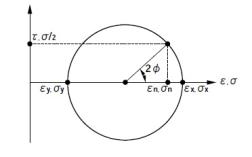前節の図3.1は、仮想の滑り面を考えるときの、垂直応力と剪断応力の計算原理を示しました。座標軸xは、この図では右向きです。右端のx軸に垂直な面を左回りに角度φで回転させた面について、垂直応力度σｎと剪断応力度τの計算式は、釣り合い条件から下のように表すことができます；
ここでの剪断応力度τの式には、マイナス(−)符号がつきます。これは、上の項で説明したように座標軸ｙの正の向きを上向きとしていますので、図3.1で見ると、τが右下向きになっていることを表しています。二次元弾性体として上下方向にσｙが作用する場合と合わせて、垂直応力度と剪断応力度を求めると、右上を向いている仮想の斜面の応力度は、下の式です。
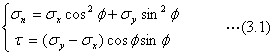
この式を変形して、下のように書き直します。
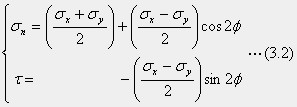
式(3.2)のσとτの意味を幾何学的に理解するための図をモール円(C.O.Mohr,1835-1918)と言います。垂直水平二方向の主応力を受けている状態から、或る面の主応力度と剪断応力度を理解するための図式方法です。角度を2φで使うことを注意します。この図を逆に応用して、或る二次元の応力状態（σＸ，σＹ，τ）から、主応力の大きさと主軸の向きを求めることができます。この説明は3.2.7項です。