目次ページ 前ページ 次ページ
2. 簡単なトラスの応力と変形
2.2 簡単な不静定トラス
2.2.1 解析の原理
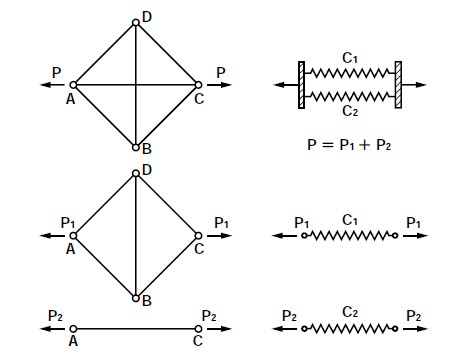不静定トラスを解くときの方法は、まず、全体の部材数と接点数とから、不静定の次数を求めます。それから、不静定次数だけの本数の部材を選んで、これを仮に取り外した状態を考えます。これを、静定基本系と言うことにします。取り外す部材を不静定部材と言い、そこに作用していた内力を不静定力とし、分解した静定基本系と不静定部材に外力として作用させます。部材を切断すると、内力は符号反対の外力の対で考えることに注意します。ここでは、図2.11に示すような、45°傾けた正方形枠と十字型に組んだ部材で構成した、１次の不静定トラス(a)を例題にして説明します。この構造は、水平部材(c)を取り外すと、静定基本系(b)になって、釣り合い条件だけで部材力を解くことができますし、変形も計算できます。元の不静定トラスは、静定基本系と不静定部材との組み合わせ構造と見て、それぞれは、バネの作用でモデル化ができます。元の不静定トラスは、前章1.2.2節で紹介した並列バネ系でモデル化ができます。静定基本系をバネ作用にモデル化するときは、前節で解説したように、静定トラスを解く必要があります。元の不静定トラスに作用させる外力は、左右を引張る状態を図示しましたが、上下の外力の対が作用する場合に簡単に応用できます。さらには、その二つの荷重条件を重ね、上下に圧縮、左右に引張の外力を作用させる場合の解を求めることができます。次数の大きい不静定構造物の解析は、橋梁構造などの専門ごとに固有の問題があります。ここでは、不静定トラスの原理が分かるような、図2.11に示すような単純な一次の不静定トラスを例として説明します。このような外力の作用は、次の第４章で、剪断変形を計算するときに考えますので、ここでは、その予備知識になるような例題を取り上げました。この静定トラスの変形は、前節の図2.7を使った問題(2)を参考にして下さい。例解：
正方形の一辺の長さをＬ、この部材の断面積をＡＡ、対角線部材の断面積をＡＢ、両部材のヤング率を同じＥとします。図ｂの静定トラスを左右にＰ１で引っ張ると、垂直部材は同じ大きさのＰ１の圧縮力が作用します。二頂点AC間の変位δ１は、図2.7の解法を参考にして求めます。水平な不静定部材を単独に引っ張るときの伸びδ２の計算式も並べて示します。
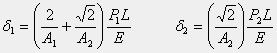
元の不静定トラスとしての変位は下の式で得られます。
