目次ページ 前ページ 次ページ
2. 簡単なトラスの応力と変形
2.1 静定トラス
演習例題 2.1(続2）
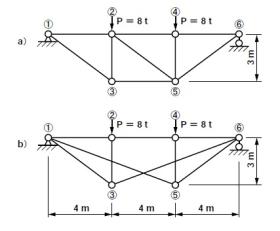(5)図2.8に示す二つの平面トラスにおいて、まず、静定・不静定の判別をせよ。ついで、部材断面積を決定し、全重量を積算せよ。ただし、許容応力度は、引張・圧縮に対して、900kgf/cm2・400 kgf/cm2、単位重量は7850 kg/m3とする。解説：
・上下のトラス構造、共に部材数Ｍ＝9、格点数Ｎ＝6ですので静定トラスです。上のトラス組みは、この章の始めに紹介した図2.1を180°回転した形式です。下の図では、３本の上弦材の圧縮力がすべて同じ、上の図では右側２本の上弦材の圧縮力が同じになることを、釣り合い条件で勘案します。
・複雑なトラス構造の計算では、格点と部材に番号付けをし、表の形で計算書をまとめると、見通しが良くなります。どのような順に番号を付けるかに関しても、かなり工夫が必要です。有限要素法（FEM）の場合、要素の自動分割法などに多くの研究があります。下の表計算で例解を示します。
・例題トラスの外力は、左右対称になるようにしてあります。これは、死荷重を作用させるときの、一つのモデルです。トラス(a)では、部材番号5の応力は0です。計算上はこの部材を必要としませんが、これを省くと不安定トラスになります。実構造の設計では、ここをダブルワーレンのＸ形に組み、部材長さから決まる、最小の細長比の断面を使います。この解説は第４章、4.2.8項で扱います。したがって、材料重量は、ここでの理論計算値よりも大きくなります。
・実務の設計では、例えば、山形鋼のカタログなどから、所要断面積を満たす材料を選ぶのが普通です。カタログには単位長さ重量が載っていますので、それを使って材料の積算をします。部材力の物理的な単位は力です。理論にこだわるとニュートン単位で計算したくなるのですが、材料の積算は重量を使うことが常識ですので、実務では、最初から力の単位系にも重量単位(kgf, tfなど)を使います。
・例題のトラス構造(b)の上弦材は、一直線になっています。垂直材はこれと直交していますので、もしここに外力が作用しなければ、垂直材の応力は0です。この垂直材が接続する上弦材は圧縮材ですので、垂直材を使うことで、座屈を考えた圧縮材の許容応力度が低くならないようにする目的があります。
・トラス(a)の格点Aは斜材がありますので、外力が片側に載ると、斜材2-5に応力がでます。演習としてP2=8tf、P4=0の条件で解いてみて下さい。
・トラス(b)では、部材が図形的に交差しますが、力学仮定は交点での部材の結合はないとします。しかし、実構造では、部材の振れを抑えるように止めるか、格点としての構造を持たせます。ダブルワーレンのＸ形に組む場合も同じです。ダブルワーレンに組むと、不静定次数が増えます。実務では、圧縮材になる側の部材を無視して、静定トラスとして解いて断面を決定します。
・トラスの変形を幾何学的に計算して求める方法は、やや難しくなります。この計算は構造力学として扱いますので、ここには含めませんでした。
図2.8aのトラス計算
部材番号 |
接続格点 |
部材長 |
部材力 |
所要断面積 |
単位長重量 |
材料重量 |
|
|
(m) |
(tf) |
(cm2) |
(kg/m) |
(kg) |
1 |
1-2 |
4.0 |
−10.7 |
26.75 |
21.0 |
84.0 |
2 |
1-3 |
5.0 |
13.3 |
14.78 |
11.6 |
58.0 |
3 |
2-3 |
3.0 |
−8.0 |
20 |
15.7 |
47.1 |
4 |
2-4 |
4.0 |
−10.7 |
26.75 |
21.0 |
84.0 |
5 |
2-5 |
5.0 |
0 |
|
|
|
6 |
3-5 |
4.0 |
10.7 |
11.89 |
9.3 |
37.2 |
7 |
4-5 |
3.0 |
−8.0 |
20 |
15.7 |
47.1 |
8 |
4-6 |
4.0 |
−10.7 |
26.75 |
21.0 |
84.0 |
9 |
5-6 |
5.0 |
13.3 |
14.78 |
11.6 |
58.0 |
|
|
|
|
|
|
499.4 |
図2.8bのトラス計算
部材番号 |
接続格点 |
部材長 |
部材力 |
所要断面積 |
単位長重量 |
材料重量 |
|
|
(m) |
(tf) |
(cm2) |
(kg/m) |
(kg) |
1 |
1-2 |
4.0 |
−10.7 |
26.75 |
21.0 |
84.0 |
2 |
1-3 |
5.0 |
8.9 |
9.9 |
7.8 |
39.0 |
3 |
2-3 |
3.0 |
−8.0 |
20 |
15.7 |
47.1 |
4 |
2-4 |
4.0 |
−10.7 |
26.75 |
21.0 |
84.0 |
5 |
1-5 |
8.54 |
7.59 |
8.4 |
6.6 |
56.4 |
6 |
3-6 |
8.54 |
7.59 |
8.4 |
6.6 |
56.4 |
7 |
4-5 |
3.0 |
−8.0 |
20 |
15.7 |
47.1 |
8 |
4-6 |
4.0 |
−10.7 |
26.75 |
21.0 |
84.0 |
9 |
5-6 |
5.0 |
8.9 |
9.9 |
7.8 |
39.0 |
|
|
|
|
|
|
537.0 |