栚師儁乕僕 丂慜儁乕僕 丂師儁乕僕
2.丂娙扨側僩儔僗偺墳椡偲曄宍
2.1丂惷掕僩儔僗
墘廗椺戣丂2.1(懕侾乯
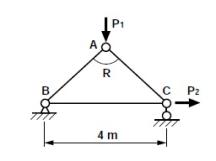 (4)恾2.7偵帵偡嶰妏宍偺僩儔僗慻傒偵偍偄偰丄晹嵽偼偡傋偰抐柺愊10 cm2偺峾朹偲偡傞丅俹侾亖10tf丄俹俀亖15 tf偲偟偰奿揰偺曄埵傪寁嶼偣傛丅嶰妏宍偺捀揰俛偺妏搙偼兤亖45亱偲偡傞丅
(4)恾2.7偵帵偡嶰妏宍偺僩儔僗慻傒偵偍偄偰丄晹嵽偼偡傋偰抐柺愊10 cm2偺峾朹偲偡傞丅俹侾亖10tf丄俹俀亖15 tf偲偟偰奿揰偺曄埵傪寁嶼偣傛丅嶰妏宍偺捀揰俛偺妏搙偼兤亖45亱偲偡傞丅椺夝丗
嶰妏宍偺捀揰俙偺妏搙傪90搙偲偟偰偄傑偡丅奜椡俹侾偵傛傞晹嵽AB,AC偺埑弅椡俹俙俛丆俹俙俠偼丄
丂丂俹俙俛亖俹俙俠亖俹侾乛2 sin45亱亖7.07 tf
偙傟偵傛傞晹嵽BC偺堷挘椡俹俛俠偼丄
丂丂俹俛俠亖俹俙俛cos45亱亖5.0 tf
丂丂冃俙俛亖冃俙俠亖亅7070/10 亖亅707 kgf/cm2
丂丂冃俛俠亖(5000+15000)/10 亖 2 000 kgf/cm2
丂丂兠俙俛亖兠俙俠亖(-707/2.1亊106)亖亅337亊10-6
丂丂兠俛俠亖(2000/2.1亊106)亖952亊10-6
丂捀揰俙偺悅捈偍傛傃悈暯偺曄埵偼丄峔憿椡妛揑偵偼僄僱儖僊乕朄偱寁嶼偟傑偡偑丄偙偙偱偼丄嫵堢栚揑傪娷傔偰丄婔壗妛揑側曽朄偱寁嶼偡傞偙偲傪椺帵偟傑偡乮嶲峫偲偟偰僄僱儖僊乕朄偵傛傞寁嶼曽朄傕壓偵帵偟偰偁傝傑偡乯丅捀揰俙偼丄晹嵽AB埑弅偱抁偔側傞偙偲偲丄捀揰俛傪夞揮拞怱偲偟偰旝彫妏搙儮俛偩偗塃夞傝偵夞揮偡傞偙偲偵場傞堏摦偲傪廳偹崌傢偣傑偡丅寁嶼偺棟榑幃偼丄幃2.4偱偡丅捀揰俛偺妏搙曄壔傪媮傔傑偡偺偱丄a仺b仺c仺a偲A仺B仺C仺A偲弴憲傝偵曄峏偟偰棙梡偟傑偡丅
丂丂晹嵽挿丗a亖b亖2/cos45亱亖2.83m丄c亖4.00m
丂丂晹嵽榗傒丗兠a亖兠b亖亅337 亊10-6丄兠c亖952亊10-6
丂丂
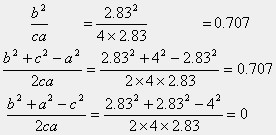
丂丂
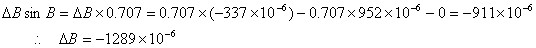
捀揰俙偺堏摦偼擇偮偺惉暘偱寁嶼偡傞丅
丂丂晹嵽AB偺挿偝偺曄壔丗儮俴亖倐兠b亖283亊(亅337 亊10-6)亖亅0.095cm
丂丂晹嵽AB偑夞揮偡傞偙偲偵傛傞捀揰俙偺捈岎曽岦偺曄埵丗倐儮俛亖283亊1289亊10-6亖0.365cm
丂丂捀揰俙偺悅捈曄埵丗丂兟倁亖儮俴亊sin45亱亅倐儮俛cos45亱亖亅0.325cm丟壓岦偒偺曄埵
丂丂捀揰俙偺悈暯曄埵丗丂兟俫亖儮俴亊cos45亱亄倐儮俛sin45亱亖亄0.191cm丟塃岦偒偺曄埵
捀揰俠偺悈暯曄埵丗丂丂丂兟俫亖們兠c丂丂丂丂丂丂丂丂丂丂丂 亖亄0.381 cm丟塃岦偒偺曄埵
丂丂丂乮旛峫丗捀揰俠偺悈暯曄埵偼丄捀揰俙偺悈暯曄埵偺俀攞偵側傞偙偲偑専嶼偵側偭偰偄傑偡乯
晹嵽 |
抐柺愊 |
晹嵽挿 |
P1亖1偵傛傞墳椡(tf) |
P1亖10丄P2亖15偵傛傞墳椡(tf) |
僄僱儖僊乕朄偵傛傞潥傒偺寁嶼 | |
丂 |
嘆 |
嘇 |
嘊 |
嘋 |
嘊亊嘊亊嘇/嘆 |
嘊亊嘋亊嘇/嘆 |
AB |
10 |
283 |
-0.707 |
-0.707 |
14.15 |
141.46 |
AC |
10 |
283 |
-0.707 |
-0.707 |
14.15 |
141.46 |
BC |
10 |
400 |
+0.500 |
20.00 |
10.00 |
400.00 |
儼 |
丂 |
丂 |
丂 |
丂 |
38.30 |
682.92 |
兟倁 |
丂 |
丂 |
丂 |
丂 |
0.182 |
0.325 |