目次ページ 　前ページ 　次ページ

2.　簡単なトラスの応力と変形

2.1　静定トラス

2.1.4　内的に静定で安定である条件

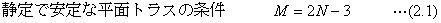
　トラスの解析方法は構造力学の課題ですので、ここでは深入りしません。しかし、静定と安定の理解は重要ですので、原理について解説しておきます。平面トラスは、幾何学的に三角形に組み上げる方法を繰り返して構成します。既に位置が決まっている２格点から２本の部材を使えば、新しい格点の位置が決まります。つまり、すでに在る部材数（Ｍ）に二本を追加すれば、格点数（Ｎ）が一つ増えます。最初の三角形はＭ＝Ｎ＝３ですので、単独に取り出して静定で安定なトラスの条件は、丸暗記しなくても、次の式が簡単に誘導できます。
　　
　同じ考え方を立体トラスでも応用できます。独立に取り出して静定で安定な立体トラス組みは三角錐状の構造であって、部材数Ｍ＝６、格点数Ｎ＝４です。既に決まっている３格点から３本の部材を使うと新しい格点が一つ増えます。
　　
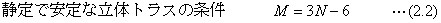
　上の構成原理で組み上げたトラス構造は、内的に安定(static)で静定(determinate)であると言います。ただし、全体図形は、形を保ったまま移動や回転ができます(mobile)ので、外的には不安定です。この単独構造で、どれか一本でも部材を取り去ると、どこかのヒンジ回りに自由な回転ができるようになって、元の形を保つことができません（不安定）。逆に、どれかの２格点を結ぶように余分の部材を追加すると、このトラスは追加部材数だけの不静定次数のトラスになります。これは、トラスに外力を作用させて部材の応力を計算するとき、力の釣り合い条件だけで解くことができなくて、不静定次数個の弾性条件を立てなければなりません。
科学書刊株式会社:電子版　「橋梁＆都市 PROJECT: 2011」
前ページ 　次ページ