目次ページ 前ページ 次ページ
1. 引張材と圧縮材
1.4 温度応力・残留応力などの不静定問題
1.4.1 解説
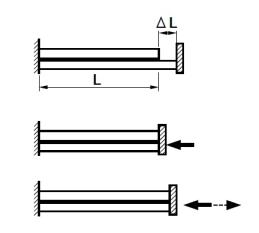二つの材料の組み合わせで作られている部材があって、一方が他方に較べて温度差があると、そのままではは歪みに食い違いができます。一体化になっているときは、この歪みを打ち消すように内部で応力の変化が生じます。この問題を解く考え方を説明します。1)まず、二つの材料の、相互の結合を緩めて、自由に変形させます。
2)温度差応力を計算するときは、温度膨張係数を使います。鋼材、コンクリート材では、α＝1.2×10-5/℃です。
3)次に外から仮の力を作用させて、この変形を無くすようにします。図1.11では下側の部材に圧縮力を作用させますが、上の部材に引張り力を作用させても結果は同じになります。このときの応力度は、σ＝ｔαＥ、力はＰ＝σＡです。
4)この状態で二つの材料を結合します。そうしておいて、外から加えている力を抜きます。これは、合成した全断面に、反対向きの力を加えます。例図では引張り力を加えます。この手順を一つの計算式にまとめるよりは、手順に沿って数値計算をする方が分かり易いでしょう。
材料内部での応力分布は、実際にはよく分からないことが多いものです。力学モデルとして、もし部材を自由にしておけば生じるであろう歪みを考えます。これには材料の乾燥収縮などがあります。履歴が分からない応力が残っているとき、これを残留応力と言います。