目次ページ 前ページ 次ページ
1. 引張材と圧縮材
1.3 偏心載荷を考える簡単な組み合わせ構造
演習例題 1.3
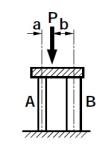(1)図1.8に示すように２本の柱の圧縮力はどのような割合になるか？ ただし、曲げなどの影響は考えないとする。Ｐの位置を考えて柱の応力を求めよ。（解説）第一義的には荷重Ｐの作用位置で比例配分した圧縮力が作用します。柱の曲げ剛性も考えてラーメン構造を考えると、３次の不静定構造ですので、弾性条件を考えて解かなければなりません。実際の構造物は、なるべくなら不静定次数が０になるように設計します。この構造では、柱を橋脚とし、その上に単純梁を載せるような力学モデルを考えます。力学的に単純化してモデルの例を以下の問題にしました。
図1.9
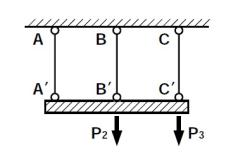(2)三本の等しい鋼棒で、剛体と見なせる梁を等間隔で吊り下げます。図1.9に示すように、荷重Ｐ１、Ｐ２を作用させたときの鋼棒の応力を求めよ。（解）部材の応力をＰＡ，ＰＢ，ＰＣとする。
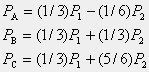
（解説：この構造構成は、構造力学的に見れば不静定です。しかし、実践的に解くときは、重ね合わせの方法を使います。中央に荷重が作用しているとき、外力は３等分されて鋼棒に伝わります。Ｐ２の外力は、左右に±Ｐ２/2と中央にＰ２を作用させた場合との和で合成します。重ね合わせの方法が使えるのは線形弾性の場合に限る便利な方法です。）
(3)上の問題で、鋼棒BB'の断面積が他の鋼棒の２倍であるときの応力を求めよ。
（解）部材の応力をＰＡ，ＰＢ，ＰＣとする。
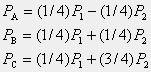
（解説：この構造も左右対称ですので、弾性方程式を考えるまでもなく、重ね合わせの方法で解くことができます。）
図1.9
(4)上の問題をさらに拡張して、４本の鋼棒を等間隔に配置した場合の鋼棒の応力を求めよ。（解）
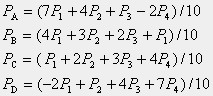
（解説：弾性方程式を立てて不静定構造として解きます。演習のために釣り合い条件と弾性条件の式を考えて解いて下さい。梁の曲げ剛性が充分に大きい場合には、曲げ部材に偏心軸力が作用するとして解くのが簡単です。この扱いは、第４章で説明します。圧縮力が作用するとき、部材の応力を０とする場合の解も考えて下さい）