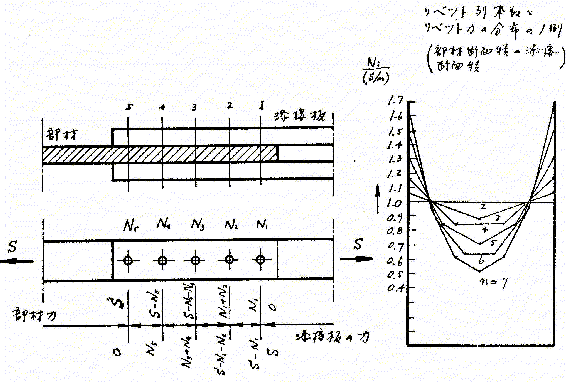
 リベット継手の力の作用方向に数本のリベットが一列に並んで配置されている場合、これらのリベットそれぞれが受け持つ力は実際には等しくなりません。もし、すべてのリベットが同じ力を伝達すると考えますと、板に作用している力は、リベット一本ごとに階段状に減少して相手材に伝えられ、相手材は同じくリベット一本ごとに階段状に力が増加します。しかし、板の応力によるひずみを考えますと、リベット穴の位置は相対的にズレを生じ、そのズレはすべてのリベット穴で同じではありません(図5)。
リベット継手の力の作用方向に数本のリベットが一列に並んで配置されている場合、これらのリベットそれぞれが受け持つ力は実際には等しくなりません。もし、すべてのリベットが同じ力を伝達すると考えますと、板に作用している力は、リベット一本ごとに階段状に減少して相手材に伝えられ、相手材は同じくリベット一本ごとに階段状に力が増加します。しかし、板の応力によるひずみを考えますと、リベット穴の位置は相対的にズレを生じ、そのズレはすべてのリベット穴で同じではありません(図5)。図5 リベット列に作用するリベット力の分布
 リベット継手の力の作用方向に数本のリベットが一列に並んで配置されている場合、これらのリベットそれぞれが受け持つ力は実際には等しくなりません。もし、すべてのリベットが同じ力を伝達すると考えますと、板に作用している力は、リベット一本ごとに階段状に減少して相手材に伝えられ、相手材は同じくリベット一本ごとに階段状に力が増加します。しかし、板の応力によるひずみを考えますと、リベット穴の位置は相対的にズレを生じ、そのズレはすべてのリベット穴で同じではありません(図5)。
リベット継手の力の作用方向に数本のリベットが一列に並んで配置されている場合、これらのリベットそれぞれが受け持つ力は実際には等しくなりません。もし、すべてのリベットが同じ力を伝達すると考えますと、板に作用している力は、リベット一本ごとに階段状に減少して相手材に伝えられ、相手材は同じくリベット一本ごとに階段状に力が増加します。しかし、板の応力によるひずみを考えますと、リベット穴の位置は相対的にズレを生じ、そのズレはすべてのリベット穴で同じではありません(図5)。
この問題を、簡単な仮定のもとに理論的に解くことができます。その仮定とは、リベット穴のズレが、リベットに作用するせん断力に比例する、および、リベット間での板のひずみがその間の平均応力に比例する、というものです。式の形は階差式になります。寸法や弾性係数などで数値計算の値は相違しますが、傾向としては次のことが言えます。
以上の理論的な根拠に従えば、最後の項目 5 を満たすような継手が最善ということになります。実際の構造ではこの状態を満足しませんので、リベット荷重は平均値の10〜25%の不均等さはあるものと考えられます。継手の静的な強度を実験した多くの例から、継手の最終強度は、リベットの配列、配置には殆ど関係がなく、リベット一本当たりのせん断強度、もしくは支圧強度にリベット本数を乗じた強度が得られています。このことは、破壊時には材料の降伏と共にリベット荷重の再配分が行なわれ、結局すべてのリベットが同一の耐荷力に達して、始めて全体の継手が破壊されるためです。
一方、継手の疲労に関しては、応力の集中が強度に大きく影響しますので、不均等なリベット荷重が生じないような注意が必要です。すなわち、強度の大きい鋼材を弱いリベットで繋ぐと、一列当たりのリベット本数が増すことになりますが、そうすると端部のリベット荷重が大きくなって、端のリベットから各個撃破で破壊が進む危険を持っています。このことは、一列のリベット本数があまり多くならないように鋼種と板厚に見合ったリベット径を選択しなければならないことを意味します。