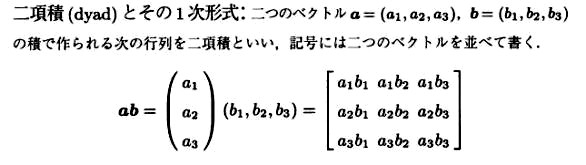
ベクトルは、力学と関連を持ち、向きと大きさを持つ量として、図に描いて感覚的に理解ができます。座標系を決めて、初めて成分の大きさが具体的に確定します。マトリックスは、ベクトルと演算させてベクトルを求める演算子的な使い方をしますので、マトリックス全体を単独の力学量として理解することができません。マトリックスは、行と列に並べた複数の成分で表しますが、この成分をテンソルと説明することがあります。筆者が学生時代、テンソルを理解しようと多くの数学参考書を読み較べてみましたが、どれも抽象的な説明に終始していて、どうしても納得が得られませんでした。力学的・幾何学的な意味づけをするよりも、マトリックスは、「ベクトルと演算させるとベクトルが得られる」、そういう数学量であると考えることで楽になりました。そうすると、演算が一意に決まるような約束が必要です。これが線形代数、つまり、ベクトルとマトリックスを使う数学です。最も単純なマトリックスの成分構成は、二つのベクトルについて、成分を積の形で含む形であって、dyad(二項積)と言います。例えば三次元の二つのベクトルを考えると、式17.1のように表します。表記法としては、二つのベクトルを並べて書きます。一般的な数式の場合は、変数を並べて書くと「掛け算記号を省く」と解釈します。幾何ベクトルの場合には、積の約束に外積(ベクトル積)と内積(スカラー積)がありますので、積の演算を保留する二項積であるか、積の演算をさせるかを区別する表記上の約束が必要になりました。明示的に表すとき、左右ベクトルを中点(・)で繋ぐときスカラー積、掛け算記号(×)を使うときはベクトル積、何も無いときは積の演算を保留した二項積とします。この約束の延長は、複数のベクトルを並べる数学量として三項積以上を定義できます。二項積を構成する二つのベクトルが座標軸を表す単位ベクトルであると、式17.1のマトリックス成分9個の中、一つだけが1で残りは0です。この二項積を一つの数学量としたものがテンソルです。
式17.1 二項積の定義
2009.5 橋梁&都市PROJECT |