目次ページ 前ページ 次ページ
2. 図形要素の代数的表現
2.3 線分・直線・面の表し方
2.3.6 幾何学的な平面はもっと実感し難いこと
幾何学で言う平面は、平面的に広がった位置を表す概念であって、実体はありません。平面は、水面や家具などの表面で実感できます。しかし、これは、平面の性質を持った実体であって、幾何学的平面そのものではありません。透明なガラス板は、光が自由に通り抜けられますので、次善の平面モデルに使います。構造物をはじめ、立体的な品物の表面は、殆どは平面で構成されていますので、図学的に扱うときは多面体モデルで考えます。紙は表・裏の区別があります。立体の表面はすべて表（おもて）扱いです。表・裏は、位相幾何学的な性質であって、座標系の約束と同じように、面に向きを決める約束です。平面上の位置を特定するには座標系の助けを必要とします。空間的には、式2.3に示す同次式を考えます。
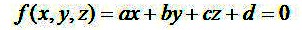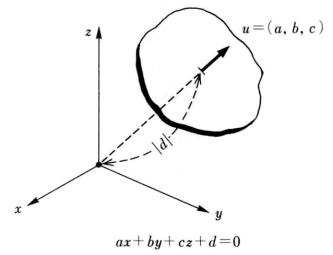
(2.3)この式は、二次元直線の式(2.1)の次元数を２から３に拡張した形になっていますし、また、式の解釈も似たように拡張します。平面上に在る点は、三つの座標(x,y,z)の中の二つ、例えば(x,y)を与えてzを求める「z=ax+by+c」の形が、代数的には一つの標準です。曲面を表す場合には、右辺がx,yの高次式になります。この形では、面がx-y座標平面に垂直に近くなったときの扱いに困ります。そこで、式(2.3)の定数(a,b,c)を単位ベクトルの成分になるように標準化します。そうすると、式(2.3)に任意の座標を代入したときのf(x,y,z)の値は、その点の、面に対する符号付の距離が得られます。符号の正負は、その点が面の表側に在るか、裏側に在るかの区別に使うことができます。ｄの値は、原点(0,0,0)が面のどちら側に在り、その距離がどれだけあるかを示す数になります（図2.3）。無限に広がっている面の存在は、面の一部を紙のような実体にモデル化して見取り図に描くことにしました。
