図2.2 空間直線の定義を示す見取り図
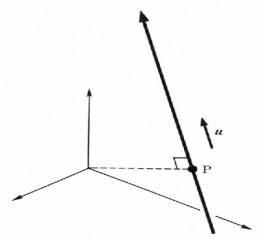 平面幾何学の直線は、何かの平面に描いた直線の図形として理解することができます。しかし、三次元空間の任意の直線は、眼に見えるような、具体的な実体で捉え難いところがあります。建設現場では、水糸やさげふりを使って水平や垂直の位置決めをします。糸を使うにしても、一般的な空間直線（ここでは線分と言うべきでしょうが）を身近に感じる機会は殆どありません。我々の居住空間は、殆どが縦・横・高さ方向に直交する空間直線で構成されていますので、任意の向きに無限に伸びる空間直線を扱うことは稀です。眼を広い外界に向けます。地図に表示してある緯度・経度・三角測量網・赤道・北回帰線などの線は、実際にその場所に行って見ることができる線ではありません。天文観測で星の位置を見るとき、望遠鏡を向ける方向は自分の居る位置を基準とした空間直線を定義しますが、この場合は天球座標系を使いますので、デカルト座標の考え方とは異なっています。空間直線そのものは捉えどころが無いのですが、直線が平面などと交わるところの点を扱うことで間接的に直線の存在を意識します。その代表的な応用が投影図です。空間直線を代数的に定義したいときは、空間の二点を結ぶとして決めるのが実践的な方法です。計算幾何学的には、基準点の座標と直線の向きを与える単位ベクトルの対に直します（図2.2）。表2.1に示した三次元の直線の型は、この約束を使って定義しました。ただし標準化の約束を加味してあります。それは、基準点の位置は原点からの距離が最小になる直線上の点を表す位置ベクトルpとし、直線の向きは単位ベクトルuで与えます。そうすると、pとuは直交します。この空間直線上の任意の位置は、基準点からの符号付距離tを使って表すことができます。この式の形は、二次元の直線の場合の式(2.2)と同じです。空間図形は、投影図に描いて感覚的に理解します。正確な情報が得られるように投影するには少なくとも二つの平行投影図が必要ですが、これを一つの投影図で済ますのが、通称で言う見取り図です（図2.2）。
2008.2 橋梁＆都市PROJECT |