目次ページ 前ページ 次ページ
2. 図形要素の代数的表現
2.3 線分・直線・面の表し方
2.3.2 直線を代数式で表す種々の方法
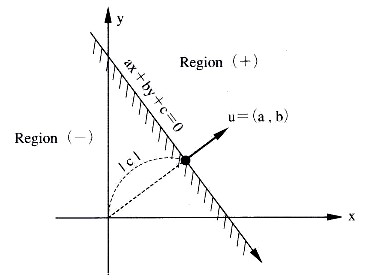中学校の数学では、(x,y)座標系を使って、直線の式を「y=ax+b」の形で習います。この式を巡って、種々の説明が教科書や参考書に書かれています。補助的に(x,y)座標系で表した図を使って、「aは直線の勾配、ｂは直線がy軸と交わるときのy座標」と教わります。この表し方であると、直線の勾配が大きくなってy軸と平行に近くなったときに困ります。そのときは「x=cy+d」に直して考えます。そうすると、式の表し方を場合に応じて取り替えることになります。どのような向きであっても利用できる式の形は何種類も提案できますが、ここでは、下の式(2.1)に示すような同次式(homogeneous expression)を考えます。
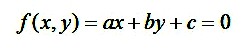(2.1)この表し方は、定数を三つ使います。全体の式を定数倍しても直線関係は保存されますので、定数間に、幾何学的な性質を持たせる条件を付けます。結論から言うと、ある基準点を通り、直線の向きを単位ベクトルuで指定します。図形として無限に連続している平面直線を見るとき、直線に向きを考え、その向きに立って直線の左右を区別します。代数式「y=ax+b」の形は、暗黙の了解で直線を右向き(+x軸方向)と考えていて、直線に対する相対的な位置関係を上下の用語で区別しています。ここに位相幾何学的な考え方が入ります。