S.18 Cardioid, Nephroid, Archimedean Spiral, Clothoid

　簡単な数学関数の応用で得られる幾何学図形の幾つかを例示しました。プログラムそのものは短いものです。この例題のCardioid とNephroidとは、 FILE/DataSaveメニューでメタファイルに作成すると、円を描くデータが並びます。DataReadメニューで読み出して結果を比較すると面白いでしょう。円の塗りつぶしのモードを、メニューからLine,　FillStyle,　Transparentの順で設定しておいて、DataReadメニューでメタファイル読み出して結果を比較すると下の図を再現させることができます。

Public Sub Proc18() 'Cardioid etc.
    Dim ift
    ift = FormGraphic.Picture1.FillStyle '-----save FillStyle
    FormGraphic.Picture1.FillStyle = 1
    Dperas
    Dpwind 0, 0, 640
    Select Case Ivar
        Case 1: Cardioid        '---- Cardioid
        Case 2: Nephroid        '---- Nephroid
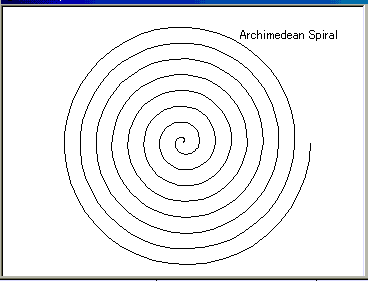
        Case 3: Archimedes      '---- Archimedean Spiral
        Case 4: Clothoid        '---- Cornu's Spiral
        Case Else: Cardioid
    End Select
    FormGraphic.Picture1.FillStyle = ift '---- restore FillStyle
End Sub
'----------------------------------------------- Cardioid
Private Sub Cardioid()
    r = 80: e = r
    For ang = 0 To 360 Step 6
        Th = ang * pie / 180
        d = e * Sqr(2 - 2 * Cos(Th))
        X = r * Cos(Th)
        Y = r * Sin(Th)
        Dpcirc X, Y, d
    Next
    Dptext 100, 200, "cardioid"
End Sub

'---- Nephroid
Private Sub Nephroid()
    r = 100: e = r
    For ang = 0 To 360 Step 5
        Th = ang * pie / 180
        d = Abs(e * Sin(Th))
        X = r * Cos(Th)
        Y = r * Sin(Th)
        Dpcirc X, Y, d
    Next
    Dptext 100, 200, "nephroid"
End Sub

'---- Archimedean Spiral
Private Sub Archimedes()
    a = 4.5
    For ang = 0 To 360 * 8 Step 8
        Th = ang * pie / 180
        r = a * Th
        X = r * Cos(Th)
        Y = r * Sin(Th)
        If ang = 0 Then
            Dpmove X, Y
        Else
            Dpdraw X, Y
        End If
    Next
    Dptext 100, 200, "Archimedean Spiral"
End Sub

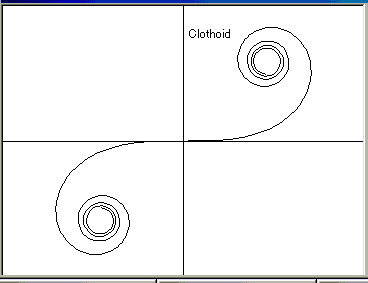
　高速道路や高速鉄道の緩和曲線として知られているクロソイドは、数学ではCornu's Spiralと呼ばれている曲線の原点付近の性質を利用したものです。

'---- Cornu's Spiral
Private Sub Clothoid()
    'Cornu's Spiral
    Dim segl, ang0, fk, tr, el, dx, dy, sc, xleft, ytop
    sc = Www * 0.25 '---- magnification factor
    xleft = Www / 2
    ytop = xleft * Gaspect0
    Dpmove -xleft, 0
    Dpdraw xleft, 0
    Dpmove 0, ytop
    Dpdraw 0, -ytop
'
    N = 200
    Th = 8 * pie    '----- four round spiral
    segl = Sqr(Th * 2) / N
    ang0 = segl * segl / 6
    For j = 1 To -1 Step -2
        Dpmove 0, 0
        X = (sc * j) * segl: Y = 0
        Dpdraw X, Y
        For i = 1 To N
            fk = 1 - 3 * i + 3 * CSng(i) * i
            ang = ang0 * fk
            tr = segl * segl * (i + i - 1)
            tr = 1 - tr * tr / 96:
            el = (sc * j) * segl * tr
            dx = el * Cos(ang)
            dy = el * Sin(ang)
            X = X + dx: Y = Y + dy
            Dpdraw X, Y
        Next
    Next
    Dptext 10, 200, "Clothoid"
End Sub