目次ページ 前ページ 次ページ
12. 三次元的に扱う弾性問題
12.3 構造力学の性質で解析する部材
演習例題 12.2
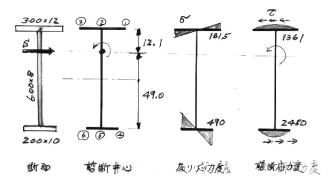
(ⅰ)水平方向の剪断力による剪断中心の計算(腹板の影響を無視します)
番号 |
板幅 |
板厚 |
横軸距離 |
剪断流面積 |
偏心距離 |
モーメント | ||
b (cm) |
t (cm) |
x (cm) |
Δ q=btx |
q |
Σ q (cm3) |
y (cm) |
yΣq (cm4) | |
1 |
0 |
0 |
||||||
1-2 |
15 |
1.2 |
7.5 |
135 |
135 |
1350 |
30.6 |
41310 |
2-3 |
15 |
1.2 |
-7.5 |
-135 |
0 |
1350 |
30.6 |
41310 |
2-5 |
60 |
0.8 |
||||||
5 |
60 |
0.8 |
||||||
4 |
0 |
0 |
||||||
4-5 |
10 |
1.0 |
5.0 |
50 |
50 |
333 |
-30.5 |
-10156 |
5-6 |
10 |
1.0 |
-5.0 |
-50 |
0 |
333 |
-30.5 |
-10156 |
| 備考 (*1): y軸回りの断面二次モーメント | Σ= |
3366 (*1) |
Σ= |
62308 | ||||
捩じり中心y座標: yC=62308 / 3366 = 18.5cm
(ⅱ)捩じり中心からの反り分布(腹板の反りは0です)
番号 |
板幅 |
偏心距離 |
反り w |
板厚 |
剪断流 q |
剪断流量 |
モーメント | |
b |
r |
Δ w=br |
ΣΔ w |
t |
∫ wt |
Q=∫q |
Qr | |
(cm) |
(cm) |
(cm2) |
(cm2) |
(cm) |
(cm4) |
(cm5) |
(cm6) | |
1 |
12.1 |
0 |
-181.5 |
|||||
1-2 |
15 |
12.1 |
181.5 |
0 |
1.2 |
1361 |
13610 |
16468 |
2-3 |
15 |
12.1 |
181.5 |
181.5 |
1.2 |
1361 |
13610 |
16468 |
2-5 |
60 |
0.8 |
||||||
6 |
-490 |
|||||||
6-5 |
10 |
49.0 |
490 |
0 |
1.0 |
2450 |
16333 |
800317 |
5-4 |
10 |
49.0 |
490 |
490 |
1.0 |
2450 |
16333 |
800317 |
| 備考 (*1):曲げ捩じれ剛性分の Cの計算 | C=Σ= |
1633570 (*1) | ||||||
(ⅲ)単純捩じれ剛性Kの計算
番号 |
板幅 |
板厚 |
剪断流 q |
b |
t |
bt3/3 | |
(cm) |
(cm) |
(cm4) |
|
1-3 |
30 |
1.2 |
17.28 |
4-6 |
60 |
0.8 |
10.24 |
2-3 |
20 |
1.0 |
6.67 |
K=Σ= |
34.19 | ||
(ⅳ)撓み角の計算
λL=500×Sqrt(0.8*106*34.19/2.1*106*1633570)=1.412
支間中央の撓み角φ (度) | |
両端拘束 |
両端自由 |
C= 0の場合:4.06 |
C= 0の場合:4.06 |
K= 0の場合:0.09 |
K= 0の場合:0.36 |
λ Lを代入: 0.16 |
λ Lを代入: 0.81 |
反りによる軸応力度は、両端自由の拘束条件の場合、支間中央で
σ=(TL/4)(w/C)
最大応力度は、下フランジ④の個所で
σ=187 kgf/cm2