図 9.10 曲げ応力度の分布（弾性と塑性）
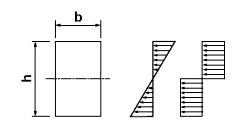構造物の設計の基本的な考え方は、実物を使って実荷重を載せる実験をして安全性を確認することです。しかし、費用と手間を考えると実用試験には向きません。実物の部材を使うことが次善の方法です。これも贅沢な試験方法ですが、説得力があります。豊富な資金に恵まれる米国で多く実施されます。この実物試験の結果から、設計で使い易いモデルを考え、それを元にして実用的な計算法を提案します。この場合の提案式は、指数関数・対数関数・三角関数などの高級な数学関数をなるべくなら使わず、また三次式以上もできれば避ける態度を取ります。この見方で、単鉄筋・腹鉄筋などの鉄筋コンクリート梁の実用設計計算式や、塑性計算の式が提案されていることを理解する必要があります。学者が提案する設計式は、高級すぎて数値計算技術からは迷惑であることが少なくありません。構造物の設計では、実用荷重で使用する場合には、最大応力度が弾性範囲内に収まるようにします。つまり弾性設計法が基本です。しかし、例外的に大きな荷重が作用して崩壊する危険を避けるため、最大、どの程度まで持つかの見積もりを踏まえます。このときに塑性設計法を応用します。鋼材の力学モデルを図9.3のように降服点を超えてから平らに移行すると仮定しても、曲げ材にすると、耐荷モーメントが降服点を超えても増加して行くこと（図9.8）に注目して下さい。梁の設計計算に応用するとき、図9.8のb点とd点の二か所で抵抗モーメントの計算を求めておいて参考にします。第４章、4.2.7項では断面係数Ｗの紹介をしました。これは、曲げモーメントによる梁の応力度分布が直線であるときの、縁応力度と抵抗モーメントの関係を表します。これとの類似で、塑性係数Ｚは、応力度分布が矩形（図9.10）であるときの定義です。
科学書刊株式会社:電子版 「橋梁＆都市 PROJECT: 2011」 |