目次ページ 前ページ 次ページ
1. 引張材と圧縮材
1.5 曲がった引張り材
解説
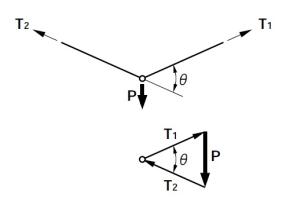

力の釣り合いは、糸を張ったモデルでの説明が良く使われます(図1.12)。折れ曲がった個所での力の釣り合いは、三角形を考えれば容易に解析できます。この場合に力は、ベクトルの計算を応用します。滑らかな曲線を描く形状は、曲線に垂直な方向の分布荷重を考えて釣り合い条件を考えます。この場合には、曲線の曲率を考えて計算しなければなりません(図1.13)。曲線を描く引張り材の例を三つあげげます。一つは、送電線の形状を表すカテナリ曲線(懸垂線:catenary)です。数学の問題として挑戦して下さい。二つ目は吊橋のケーブル形状に見るような方物線です。これは、橋梁工学で扱います。三つ目はリング状に構成する部材であって、内水圧を受けるパイプ構造の円周周りの応力であって、フープテンション(hoop tension)と言います。鉄筋コンクリート柱では、螺旋鉄筋柱の設計に応用されています。圧縮力が柱に作用するとき、半径方向にポアソン係数分の膨張を抑えるため、円周方向にリング状の鉄筋を巻きます。そうしない鉄筋コンクリートの柱よりも対荷力が上がります。曲線形の圧縮材は、アーチ構造に使いますが、こちらは部材の曲げ剛性も考える必要がありますので、ここでは説明しません。
軸力Tだけを受ける線材が曲線変形する形状の力学を考えるときは、曲線に沿って測る一次元の曲線座標sを考えます。一般的に考えると複雑ですが、多く実用されるのは円弧を描く場合です。微分方程式で表すと、

Rを曲率半径、kを曲率と言います。