目次ページ 前ページ 次ページ
4. 初等幾何学の作図例題
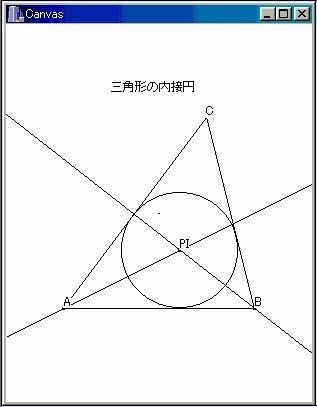
4.4 三角形の内接円を求める
 |
10 REM 三角形の内接円を求める 20 REM === 角の二等分線を求める === 30 CLG 40 DEF2PT P : DEF2ED E : DEF2CR C : DEF2LN L 50 LET PA,PB,PC=-200,-200,200,-200,100,200 60 EAB=PA @ PB : EAB1=EAB/ABS(EAB): EAB1=PA 70 EAC=PA @ PC : EAC1=EAC/ABS(EAC): EAC1=PA 80 LA=EAC1+EAB1 : REM bisector thru A 90 EBA=PB @ PA : EBA1=EBA/ABS(EBA): EBA1=PB 100 EBC=PB @ PC : EBC1=EBC/ABS(EBC): EBC1=PB 110 LB=EBA1+EBC1 : REM bisector thru B 120 PI=LA & LB : RI=DIS(PI,EAB) : LET CI=PI,RI 130 CI=CI : REM inscribed circle drawing 140 DPTEXT -100,250,"三角形の内接円" 150 LET X,Y=PA: DPTEXT X,Y,"A" 160 LET X,Y=PB: DPTEXT X,Y,"B" 170 LET X,Y=PC: DPTEXT X,Y,"C" 180 LET X,Y=PI: DPTEXT X,Y,"PI" |
図4.3 三角形の内接円を求める |
GBASICのプログラム |