S.7　Sin-Surface

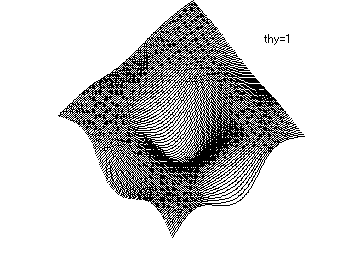
　曲面を表す式の形が z=f(x,y)の形をしている場合、これを線図で立体的に表示させる一つの方法に ScanLine法があります。これは、関数zをx-z面、もしくはy-z面に並行な面で輪切りにし、切断面の描く曲線を視点に近い方から作図させます。このとき、作図面上に、既に作図した図形を囲む領域を作っておいて、曲線がその領域の内側にあれば線を引かず、領域の外にあれば線を引くと同時に新しく作図領域を広げます。輪切りにするメッシュ間隔を狭くすると隠れ線の境界が滑らかになりますが、線の間隔が詰まり過ぎて見難い図になります。

　この方法で曲面図形を作図させるとき、３次元図形から２次元図形への投影変換が必要です。変換原理にはカメラでの撮影と同じ原理の中心投影法が自然に見えますが、望遠カメラで観察すると平行投影に近づきます。この例題では中心投影を使います。この設定は、仮想のカメラを、ある世界座標空間に置き、そこから原点を視野に納めます。曲面は中心を世界座標の原点に置くようにしますと、全体図形が程よく納まります。ただし、図形の高さによって図が多少上下または左右に触れますので、作図のウインドウ(Dpwind)を少し調整します。

Public Sub Proc7()
    '--- Surface Drawing of z=f(x,y) by ScanLine Method
    Dim Gmax(-320 To 320), Gmin(-320 To 320)
    Dim Igra

    Dim x, y, z, xi, yi, zi, xo, yo, zo, stepx, stepy, rr
    Dim ths, ss, th1, th2, thy, thz
    Dim ii, IX, iy
    Select Case Ivar
        Case 1: thy = 0.01
        Case 2: thy = 1
        Case 3: thy = 1.7
        Case 4: thy = 2.7
        Case Else: thy = 0.01
    End Select
    '------ Working mesh
    For ii = -320 To 320
        Gmin(ii) = 320: Gmax(ii) = -320
    Next ii
    Dperas
    Dpwind 0, -10, 640
    '------ Camera Position
    CamP(1) = 880
    CamP(2) = 0
    CamP(3) = 1000
    Dpcam 0.6, 0, Flen
    ths = -3 * pie / 2
    stepx = 4
    stepy = 2
    ss = 3 * pie * stepx / 400
    rr = 70
    thz = 0.7
    th2 = ths
    Igra = 0
        For IX = 200 To -200 Step -stepx
        x = IX: Igra = 0: th1 = ths
        For iy = -200 To 200 Step stepy
            y = iy
            z = rr * (Cos(th1) _
                    + Cos(th1) * Cos(th2) _
                    + Cos(th2))
            xi = x: yi = y: Rotz xi, yi, xo, yo, thz
            zi = z: xi = xo: Roty zi, xi, zo, xo, thy
            Projection xo, yo, zo
            Call Mm_graphics(Gmin(), Gmax(), Igra)
            th1 = th1 + ss / 2
        Next iy
        th2 = th2 + ss
    Next IX
    Dptext 150, 170, ("thy=" + CStr(thy))
End Sub
'=====================================================
Private Sub Mm_graphics(Gmin(), Gmax(), Igra)
    Static gx, gy, mgx As Double, mgy As Double
    gx = Int(Gxxx + 0.5): gy = Int(Gyyy + 0.5)
    If gy <= Gmin(gx) Or gy >= Gmax(gx) Then
        If Igra = 1 Then
            Dpmove mgx, mgy
            Dpdraw gx, gy
        End If
        mgx = gx: mgy = gy
        If gy < Gmin(gx) Then Gmin(gx) = gy
        If gy > Gmax(gx) Then Gmax(gx) = gy
        Igra = 1
    Else
        Igra = 0
    End If
End Sub