目次ページ 前ページ 次ページ
4. 論理学の応用場面
4.4 幾何モデリングの論理
4.4.3 平面図形の論理処理
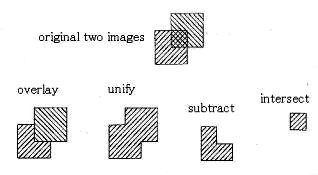コンピュータグラフィックスの作画技術は、平面図形の幾何学的処理の多様な応用で構成されています。これには、幾何モデルとして、切り紙モデルと地図モデルの二種類があります。切り紙の加工処理は、種々の形状の切り紙に切ることと、それを重ね合わせて連続した一つの形状にすることです。地図モデルは、切り紙の個別の形状の集合で、境界を考えた地図のような図形を作成することです。図4.2は、３Ｄモデルの干渉処理である和・差・積の演算に加え、重ね合わせて地図のように上描き技法を示したものです。二つの平面図形の論理処理は、第2.4節の図2.1 ベン図が原理を説明しています。ただし、その中で、論理和と論理積の二つだけが実践的な意義を持ちます。図4.2は、二つの四変形の干渉結果を図示していますが、演算原理は表4.2の場合と同じ方法を使います。切り紙モデルは、単位としては一つの連続した紙を考え、材料の有る部分と無い部分とを真偽値の(1,0)で区別しますので、二値論理学の扱いをします。なお、穴の空いた切り紙も考えられ、この穴の領域は偽の扱いです。ところで、地図モデルは、切り紙モデル全体を複数の領域に区分けした、図形としては区分地図のようになります。この図形の特徴は、領域を区切る境界線にあります。幾何モデルとして扱うときは、領域単位の図形を多角形とします。この多角形の辺は、隣り合う領域の境界線である場合と、切り紙の外形線になる場合とがあって、外形線は空の領域との境界線です。空の領域には穴の場合があります。前項で説明した多面体モデルは、面の境界となる辺は、二次元の地図モデルでの境界線と同質の図形構成要素です。しかし、この辺は、必ず隣合う多角形の境界であって、空の領域との境界は有りません。多面体の展開図を作成するときは、この多面体を張りぼてモデルに考えて、どこかの辺に沿って切り出して展開する操作をします。この図から、幾つかの領域の境界を外して行くと、最後に一つの切り紙ができます。ここでの地図モデルは、論理学的には多値モデルです。四色問題は、四値モデルで地図の領域分けの問題でもあります。
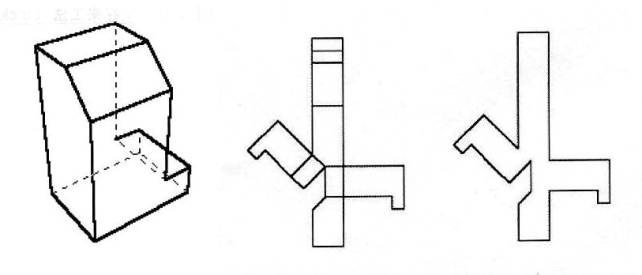
図4.3 左から多面体モデル→地図モデル→切り紙モデルへの変換