目次ページ, 前ページ, 次ページ
12. 連続桁の計算
12.5 応力の影響線
12.5.6 等断面等径間の場合の式

式12.3の逆変換の形を下のように表します。

式12.5のマトリックスの行成分(列成分でも同じです)は、不静定力の組みを表します。この力を静定基本系に作用させると、或る個所の不静定力である曲げモーメントMiの位置だけをヒンジにして、そこでの変位θiだけが単位(=1)となるような梁の変形が計算できます。また、全体変形を一定倍して、Mi=1がヒンジ位置に作用するとしたときの変形量(回転角φ)の計算ができます。等断面、等径間、三径間連続桁では、不静定次数が2です。この場合の式12.4と、その解の12.5は簡単に求まります。
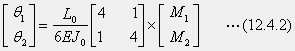
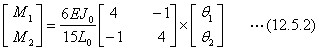
上の二つの式のマトリックスの係数から、M1=1、M2=-1が作用すると、θ1=L1/2EJ0、θ2=0となることが導かれ、梁の変形が図12.12のようになります。
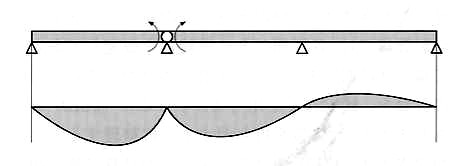
図12.12 中間支点上でヒンジを挿入し支点モーメントを作用させる力学モデル