目次ページ, 前ページ, 次ページ
12. 連続桁の計算
12.5 応力の影響線
12.5.5 不静定力を求める連立方程式
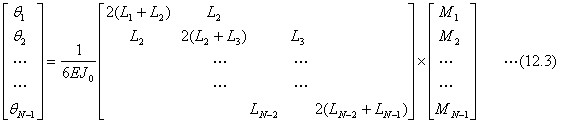
上の式で、EJ0は、どれか一つの径間での値を基準にします。大文字にしたLは換算した径間長であって、例えばL1について、下の式で計算します。なお、後の式で使うL0は、基準にした径間の径間長です。
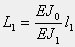
構造力学での三連モーメント式は、右辺に外力による撓み角の大きさを表す荷重項が入ります。重要な個所は、不静定力を変数とした、(N-1)次の対称な変位のマトリックスの部分です。FEM(有限要素法)の用語で言えばflexibility matrixです。この対称マトリックスは、対角線要素と、その両隣りの成分以外が0であるバンドマトリックス(band matrix)ですので、数値計算では消去法で逆マトリックスが簡単に計算できます。この逆マトリックスは、変位から不静定力を求める式になりますので、stiffness matrixに当たります。これも対称マトリックスで得られます。