吊橋に作用する横方向の変形は、おもに風荷重を考えればよく、影響線を求めるような力学モデルは必要ありません。補剛桁に作用する荷重は、等分布の風荷重と、吊材が補剛桁を斜めになるため、振り子としての復元力が作用して曲げ変形と釣合います。考え方を単純にするため、荷重と変形ともに支間方向に半波形の正弦関数を仮定します。支間中央の撓みuは下のように得られます。
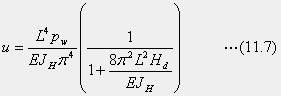 式(11.7)は、次のように解釈します。右辺の左にまとめた式は、EJHの横曲げ剛性を持つ支間Lの単純桁が等分布荷重pwによって変位する計算式です。構造力学の公式にある、5pL4/384EJに相当する計算です。右辺、括弧の中の式は、吊橋の主ケーブルが変形を抑える比率を与えます。ただし、数値計算をするときは、全橋としての力学系を考えますので、Hdは左右のケーブルの死荷重による水平反力を代入することに注意します。定常な水平振動の振動数を求めるときは、単位長さの桁の重量mによる慣性力を下のように代入することで得られます。
式(11.7)は、次のように解釈します。右辺の左にまとめた式は、EJHの横曲げ剛性を持つ支間Lの単純桁が等分布荷重pwによって変位する計算式です。構造力学の公式にある、5pL4/384EJに相当する計算です。右辺、括弧の中の式は、吊橋の主ケーブルが変形を抑える比率を与えます。ただし、数値計算をするときは、全橋としての力学系を考えますので、Hdは左右のケーブルの死荷重による水平反力を代入することに注意します。定常な水平振動の振動数を求めるときは、単位長さの桁の重量mによる慣性力を下のように代入することで得られます。
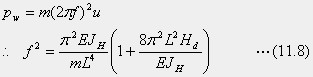 なお、数値計算の場合には、力と重量単位とのディメンション合わせを注意しなければなりませんので、慣用的には、式11.8では、mではなく(m/G)を使います。ただしGは重力の加速度です。
なお、数値計算の場合には、力と重量単位とのディメンション合わせを注意しなければなりませんので、慣用的には、式11.8では、mではなく(m/G)を使います。ただしGは重力の加速度です。
2010.2 橋梁&都市PROJECT |
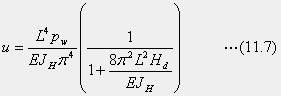 式(11.7)は、次のように解釈します。右辺の左にまとめた式は、EJHの横曲げ剛性を持つ支間Lの単純桁が等分布荷重pwによって変位する計算式です。構造力学の公式にある、5pL4/384EJに相当する計算です。右辺、括弧の中の式は、吊橋の主ケーブルが変形を抑える比率を与えます。ただし、数値計算をするときは、全橋としての力学系を考えますので、Hdは左右のケーブルの死荷重による水平反力を代入することに注意します。定常な水平振動の振動数を求めるときは、単位長さの桁の重量mによる慣性力を下のように代入することで得られます。
式(11.7)は、次のように解釈します。右辺の左にまとめた式は、EJHの横曲げ剛性を持つ支間Lの単純桁が等分布荷重pwによって変位する計算式です。構造力学の公式にある、5pL4/384EJに相当する計算です。右辺、括弧の中の式は、吊橋の主ケーブルが変形を抑える比率を与えます。ただし、数値計算をするときは、全橋としての力学系を考えますので、Hdは左右のケーブルの死荷重による水平反力を代入することに注意します。定常な水平振動の振動数を求めるときは、単位長さの桁の重量mによる慣性力を下のように代入することで得られます。
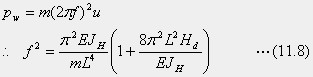 なお、数値計算の場合には、力と重量単位とのディメンション合わせを注意しなければなりませんので、慣用的には、式11.8では、mではなく(m/G)を使います。ただしGは重力の加速度です。
なお、数値計算の場合には、力と重量単位とのディメンション合わせを注意しなければなりませんので、慣用的には、式11.8では、mではなく(m/G)を使います。ただしGは重力の加速度です。